题目内容
18．从地平面A、B、C三点测得某山顶的仰角均为15°，设∠BAC=30°，而BC=200m，求山高（结果精确到0.1m）．分析 先求出△ABC的外接圆的半径R，再利用从地平面A、B、C三点测得某山顶的仰角均为15°，求山高．
解答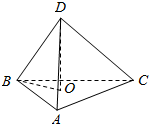 
解：由题意，先求出△ABC的外接圆的半径R，
∵∠BAC=30°，BC=200m，
∴2R=$\frac{200}{sin30°}$=400，
∴R=200，
∵从地平面A、B、C三点测得某山顶的仰角均为15°，
∴山高h=Rtan15°=200×$\frac{1-\frac{\sqrt{3}}{3}}{1+1×\frac{\sqrt{3}}{3}}$≈53.6m
点评 本题考查△ABC的外接圆的半径，考查特殊角三角函数的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
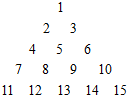把自然数1，2，3，4，…按如图方法排成一个数阵，根据如图排列规律，求数列中第n（n≥3）行从左到右的第三个数．