题目内容
17.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2,x≤0}\\{2x-6,x>0}\end{array}\right.$的零点个数是2.分析 令f(x)=0解出零点即可.
解答 解:当x≤0时,令f(x)=0得x2-2=0,解得x=-$\sqrt{2}$.
当x>0时,令f(x)=0得2x-6=0,解得x=3.
故f(x)有两个零点.
故答案为2.
点评 本题考查了函数零点的计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.图1是某学生的数学考试成绩的茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14,图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图,那么程序框图输出的结果是( )
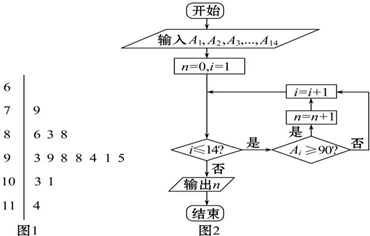

| A. | 14 | B. | 9 | C. | 10 | D. | 7 |
2.已知点P为圆C:x2+y2=4上的动点,A(4,0),则线段AP中点M的轨迹方程为( )
| A. | (x-2)2+y2=1 | B. | (x+2)2+y2=1 | C. | (x-2)2+y2=4 | D. | x2+(y-2)2=4 |
6.二项式(a-1)8的展开式中,最大的二项式系数为( )
| A. | C${\;}_{8}^{4}$ | B. | -C${\;}_{8}^{4}$ | C. | C${\;}_{9}^{5}$ | D. | -C${\;}_{9}^{5}$ |
8.已知x,y∈R+,且满足x+2y=2xy,那么x+4y的最小值为( )
| A. | 3-$\sqrt{2}$ | B. | 3+2$\sqrt{2}$ | C. | 3+$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
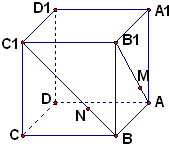 在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论:
在正方体ABCD-A1B1C1D1中,点M、N分别在AB1,BC1上,且AM=$\frac{1}{3}$AB1,BN=$\frac{1}{3}$BC1,则下列结论: