题目内容
如图,设A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为等边三角形.记以Ox轴正半轴为始边,射线OA为终边的角为θ.(1)若点A的坐标为(
 ,
, ),求
),求 的值;
的值;(2)设f(θ)=|BC|2,求函数f(θ)的解析式和值域.

【答案】分析:(1)根据A的坐标,利用三角函数的定义,求出sinθ,cosθ,再利用二倍角公式,即可得到结论;
(2)由题意,cos∠COB=cos(θ+60°),利用余弦定理,可得函数f(θ)的解析式,从而可求函数的值域.
解答:解:(1)∵A的坐标为(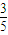 ,
,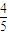 ),以Ox轴正半轴为始边,射线OA为终边的角为θ
),以Ox轴正半轴为始边,射线OA为终边的角为θ
∴根据三角函数的定义可知,sinθ=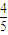 ,cosθ=
,cosθ=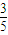 ,
,
∴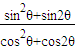 =
=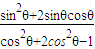 =
=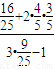 =20;
=20;
(2))∵△AOB为正三角形,∴∠AOB=60°.
∴cos∠COB=cos(θ+60°)
∴f(θ)=|BC|2 =|OC|2+|OB|2-2|OC|•|OB|cos∠COB=2-2cos(θ+60°)
∵θ∈R,∴f(θ)∈[1,3].
点评:本题考查任意角的三角函数的定义,考查余弦定理求边长的平方,考查学生的计算能力,属于中档题.
(2)由题意,cos∠COB=cos(θ+60°),利用余弦定理,可得函数f(θ)的解析式,从而可求函数的值域.
解答:解:(1)∵A的坐标为(
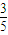 ,
,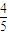 ),以Ox轴正半轴为始边,射线OA为终边的角为θ
),以Ox轴正半轴为始边,射线OA为终边的角为θ∴根据三角函数的定义可知,sinθ=
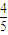 ,cosθ=
,cosθ=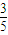 ,
,∴
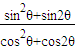 =
=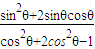 =
=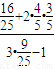 =20;
=20;(2))∵△AOB为正三角形,∴∠AOB=60°.
∴cos∠COB=cos(θ+60°)
∴f(θ)=|BC|2 =|OC|2+|OB|2-2|OC|•|OB|cos∠COB=2-2cos(θ+60°)
∵θ∈R,∴f(θ)∈[1,3].
点评:本题考查任意角的三角函数的定义,考查余弦定理求边长的平方,考查学生的计算能力,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.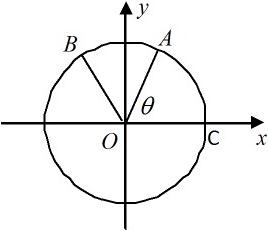 如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,
如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,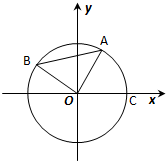 (2012•嘉定区三模)如图,设A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为等边三角形.记以Ox轴正半轴为始边,射线OA为终边的角为θ.
(2012•嘉定区三模)如图,设A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为等边三角形.记以Ox轴正半轴为始边,射线OA为终边的角为θ. 如图,设
如图,设