题目内容
已知M是△ABC内的一点,且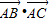 =2
=2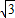 ,∠BAC=30°,若△MBC,△MCA和△MAB的面积分别为
,∠BAC=30°,若△MBC,△MCA和△MAB的面积分别为 ,x,y,则
,x,y,则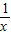 +
+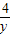 的最小值是( )
的最小值是( )A.20
B.18
C.16
D.9
【答案】分析:利用向量的数量积的运算求得bc的值,利用三角形的面积公式求得x+y的值,进而把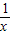 +
+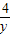 转化成2(
转化成2(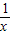 +
+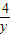 )×(x+y),利用基本不等式求得
)×(x+y),利用基本不等式求得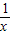 +
+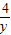 的最小值.
的最小值.
解答:解:由已知得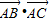 =bccos∠BAC=2
=bccos∠BAC=2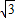 ⇒bc=4,
⇒bc=4,
故S△ABC=x+y+ =
= bcsinA=1⇒x+y=
bcsinA=1⇒x+y= ,
,
而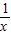 +
+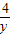 =2(
=2(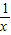 +
+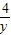 )×(x+y)
)×(x+y)
=2(5+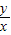 +
+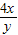 )≥2(5+2
)≥2(5+2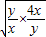 )=18,
)=18,
故选B.
点评:本题主要考查了基本不等式在最值问题中的应用,向量的数量积的运算.要注意灵活利用y=ax+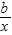 的形式.
的形式.
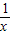 +
+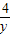 转化成2(
转化成2(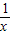 +
+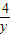 )×(x+y),利用基本不等式求得
)×(x+y),利用基本不等式求得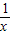 +
+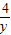 的最小值.
的最小值.解答:解:由已知得
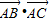 =bccos∠BAC=2
=bccos∠BAC=2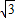 ⇒bc=4,
⇒bc=4,故S△ABC=x+y+
 =
= bcsinA=1⇒x+y=
bcsinA=1⇒x+y= ,
,而
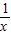 +
+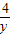 =2(
=2(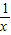 +
+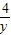 )×(x+y)
)×(x+y)=2(5+
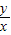 +
+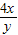 )≥2(5+2
)≥2(5+2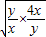 )=18,
)=18,故选B.
点评:本题主要考查了基本不等式在最值问题中的应用,向量的数量积的运算.要注意灵活利用y=ax+
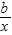 的形式.
的形式. 
练习册系列答案
相关题目