题目内容
设
，求a2+a4+…+a2n的值
- A.3n
- B.3n-2
- C.
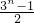
- D.
C
分析：分别令x=1，-1，0，代入展开式，即可求得结论．
解答：令x=1，则（1+1+12）n=a0+a1+…+a2n①
令x=-1，则（1-1+1）n=a0-a1+…+a2n②
∴①+②得2（a0+a2+a4+…+a2n）=3n+1
∴a0+a2+a4+…+a2n=
令x=0，则a0=1，∴a2+a4+…+a2n=-1=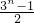
故选C．
点评：本题考查二项展开式，考查学生的计算能力，属于基础题．
分析：分别令x=1，-1，0，代入展开式，即可求得结论．
解答：令x=1，则（1+1+12）n=a0+a1+…+a2n①
令x=-1，则（1-1+1）n=a0-a1+…+a2n②
∴①+②得2（a0+a2+a4+…+a2n）=3n+1
∴a0+a2+a4+…+a2n=
令x=0，则a0=1，∴a2+a4+…+a2n=
-1=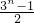故选C．
点评：本题考查二项展开式，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
，求a2+a4+…+a2n的值（ ）
，求a2+a4+…+a2n的值（ ）
