题目内容
选修4-1:几何证明选讲
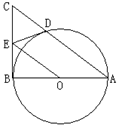
如图,圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点。
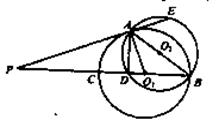
求证:(Ⅰ)PA·PD=PE·PC;(Ⅱ)AD=AE。
如图,圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点。

求证:(Ⅰ)PA·PD=PE·PC;(Ⅱ)AD=AE。
(Ⅰ)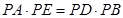 ①
①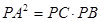 ②,由①,②得
②,由①,②得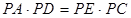
(Ⅱ)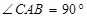 ∴
∴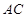 是⊙
是⊙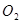 的切线由(Ⅰ)知
的切线由(Ⅰ)知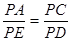 ∴
∴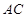 ∥
∥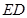 ∴
∴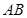 ⊥
⊥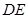 ,
, 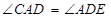
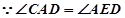 ,
,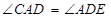 ∴
∴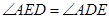 ∴
∴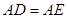
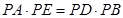 ①
①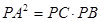 ②,由①,②得
②,由①,②得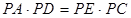
(Ⅱ)
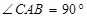 ∴
∴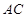 是⊙
是⊙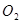 的切线由(Ⅰ)知
的切线由(Ⅰ)知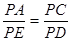 ∴
∴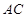 ∥
∥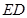 ∴
∴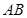 ⊥
⊥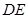 ,
, 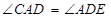
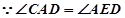 ,
,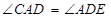 ∴
∴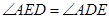 ∴
∴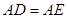
试题分析:(Ⅰ)
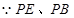 分别是⊙
分别是⊙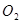 的割线∴
的割线∴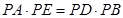 ①
①又
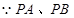 分别是⊙
分别是⊙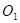 的切线和割线∴
的切线和割线∴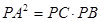 ②
②由①,②得
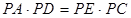 …………………… 5分
…………………… 5分(Ⅱ)连结
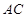 、
、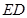
设
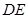 与
与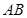 相交于点
相交于点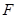
∵
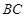 是⊙
是⊙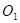 的直径
的直径∴
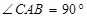
∴
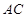 是⊙
是⊙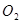 的切线.
的切线. 由(Ⅰ)知
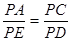 ,∴
,∴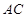 ∥
∥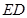 ∴
∴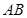 ⊥
⊥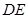 ,
, 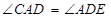
又∵
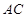 是⊙
是⊙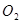 的切线,∴
的切线,∴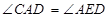
又
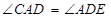 ,∴
,∴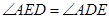
∴
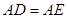 ………………………10分
………………………10分点评:此类题目较简单,学生借助于初中所学部分平面几何知识的基础容易解决

练习册系列答案
相关题目
 与⊙
与⊙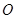 相切,
相切,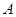 为切点,
为切点,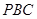 为割线,
为割线,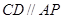 ,
,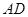 、
、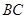 相交于
相交于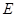 点,
点,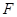 为
为 上一点,且
上一点,且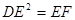 ·
·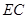 .
.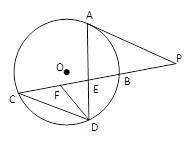
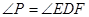 ;
;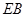 =
=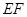 ·
·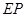 .
.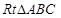 中,
中,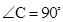 ,
,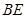 平分
平分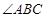 交
交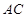 于点
于点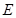 ,点
,点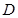 在
在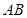 上,
上,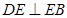 .
.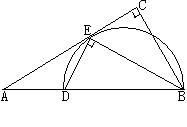
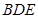 的外接圆的切线;
的外接圆的切线;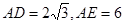 ,求
,求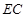 的长.
的长. 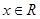 ,
,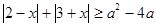 恒成立,则
恒成立,则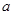 满足________.
满足________.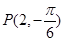 到直线
到直线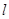 :
: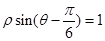 的距离是_______.
的距离是_______.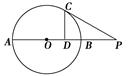
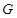 是△
是△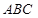 的外心,
的外心,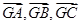 是三个单位向量,且2
是三个单位向量,且2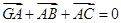 ,
,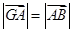 ,如图所示,△
,如图所示,△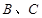 分别在
分别在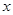 轴和
轴和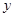 轴的非负半轴上移动,
轴的非负半轴上移动, 是坐标原点,则
是坐标原点,则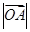 的最大值为 。
的最大值为 。
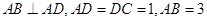 , 动点P在以点C为圆心,且与直线BD相切的圆内运动,设
, 动点P在以点C为圆心,且与直线BD相切的圆内运动,设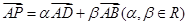 ,则α+β的取值范围是 ( )
,则α+β的取值范围是 ( )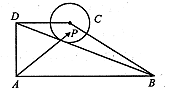
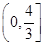
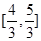
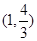
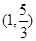
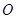 上一点
上一点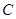 在直径
在直径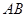 上的射影为
上的射影为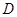 .
.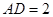 ,
,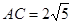 ,则
,则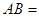 .
.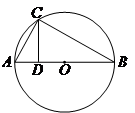
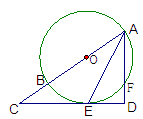
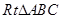 的直角边
的直角边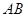 为直径作圆
为直径作圆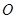 ,圆
,圆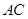 交于
交于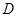 ,过
,过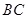 交于
交于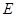 ,若
,若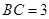 ,
,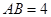 ,则
,则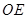 ="_________"
="_________"