题目内容
已知 ,点
,点
 在函数
在函数 的图象上,
的图象上, .
.
(1)求数列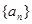 的通项公式;
的通项公式;
(2)数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,求证:
,求证: 为等差数列;
为等差数列;
(3)求 的值,使得数列
的值,使得数列 是等差数列,并求出
是等差数列,并求出 的通项公式.
的通项公式.
【答案】
(1)由于 ,
,
 .
.
 .
…………(2分)
.
…………(2分)
∴ 数列 是等差数列,首项
是等差数列,首项 ,公差d为4.
,公差d为4.
 .……………………(4分)
.……………………(4分)
(2)由 ,
,

 是等差数列,…………………………(8分)
是等差数列,…………………………(8分)
(3)由(2)知

 =
= (
( )= 4
)= 4 ∴
∴ = 0,
∴
= 0,
∴ =1,此时
=1,此时 .
.

 此时数列
此时数列 是等差数列.
是等差数列.
【解析】略

练习册系列答案
相关题目
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
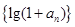 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 及数列
及数列 的通项;
的通项; ,求数列
,求数列 的前
的前 项和
项和 。
。 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; 的前
的前 项积为
项积为 ,求
,求 的通项公式;
的通项公式; 是
是 与
与 的等差中项,数列
的等差中项,数列 的前
的前 ,求证:
,求证: .
.
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 ;
; ,求数列
,求数列 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1