题目内容
已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
(1)证明数列 是等比数列;
是等比数列;
(2)设 ,求
,求 及数列
及数列 的通项;
的通项;
(3)记 ,求数列
,求数列 的前
的前 项和
项和 。
。
【答案】
(Ⅰ)由已知 ,
,

 ,两边取对数得;(Ⅱ)
,两边取对数得;(Ⅱ)
 ;(Ⅲ)
;(Ⅲ)
 .
.
【解析】
试题分析:(Ⅰ)由已知 ,
, 

 ,两边取对数得
,两边取对数得 ,即
,即
 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅱ)由(Ⅰ)知

 (*)
(*)


 =
=
由(*)式得
(Ⅲ)



又





 .
.
考点:本题考查了数列的通项及前n项和求法。
点评解决数列的前n项和的方法一般有:公式法、倒序相加法、错位相减法、分组求和法、裂项法等,要求学生掌握几种常见的裂项比如

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
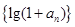 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; 的前
的前 项积为
项积为 ,求
,求 的通项公式;
的通项公式; 是
是 与
与 的等差中项,数列
的等差中项,数列 的前
的前 ,求证:
,求证: .
.
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 ;
; ,求数列
,求数列 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1