题目内容
已知 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
(1)证明:数列 是等比数列;
是等比数列;
(2)设数列 的前
的前 项积为
项积为 ,求
,求 及数列
及数列 的通项公式;
的通项公式;
(3)已知 是
是 与
与 的等差中项,数列
的等差中项,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
【答案】
(1)见解析(2)
 (3)见解析
(3)见解析
【解析】(1)按照等比数列的定义只需证明: 为定值即可.
为定值即可.
(2)根据(1)可求出其通项,进而求出 的通项,从而可得积Tn的值,
的通项,从而可得积Tn的值,
及 的通项公式.
的通项公式.
(3)先根据 是
是 与
与 的等差中项,求出
的等差中项,求出
 ,然后叠加求和即可证明.
,然后叠加求和即可证明.
解:(1)证明:由已知 ,∴
,∴ …2分
…2分
∵ ,两边取对数,得
,两边取对数,得 …4分
…4分
∴ 是等比数列,公比为2,首项为
是等比数列,公比为2,首项为 …5分
…5分
(2)由(1)得 ,∴
,∴ …6分
…6分
∵
 …8分
…8分
∴ …9分
…9分
(3)∵
 …11分
…11分
(另法:
 )
)
∴
 …12分
…12分
显然 ,∴
,∴
又 ,∴
,∴ …14分
…14分

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
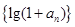 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 及数列
及数列 的通项;
的通项; ,求数列
,求数列 的前
的前 项和
项和 。
。 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 ;
; ,求数列
,求数列 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1