题目内容
如图所示,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的右侧),且|MN|=3,已知椭圆D: +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点( ,
, ).
).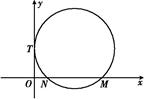
(1)求圆C和椭圆D的方程;
(2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾斜角互补.
(1)(x-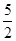 )2+(y-2)2=
)2+(y-2)2=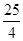
 +
+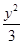 =1 (2)见解析
=1 (2)见解析
解析(1)解:设圆的半径为r,由题意,圆心为(r,2),
因为|MN|=3,
所以r2=( )2+22=
)2+22=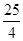 ,r=
,r=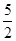 ,
,
故圆C的方程是(x-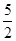 )2+(y-2)2=
)2+(y-2)2=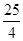 ①
①
在①中,令y=0解得x=1或x=4,
所以N(1,0),M(4,0).
由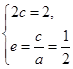 得c=1,a=2,
得c=1,a=2,
故b2=3.
所以椭圆D的方程为 +
+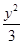 =1.
=1.
(2)证明:设直线l的方程为y=k(x-4).
由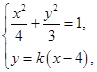
得(3+4k2)x2-32k2x+64k2-12=0 ②
设A(x1,y1),B(x2,y2),
则x1+x2=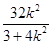 ,x1x2=
,x1x2=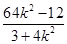 .
.
当x1≠1,x2≠1时,
kAN+kBN=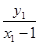 +
+
=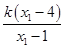 +
+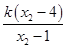
=k·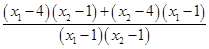
=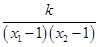 ·[2x1x2-5(x1+x2)+8]
·[2x1x2-5(x1+x2)+8]
=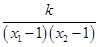 ·
·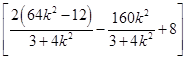
=0.
所以kAN=-kBN,
当x1=1或x2=1时,k=±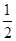 ,
,
此时,对方程②,Δ=0,不合题意.
所以直线AN与直线BN的倾斜角互补.

练习册系列答案
相关题目
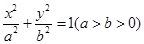 的离心率为
的离心率为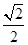 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线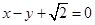 相切。
相切。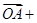
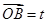 ·
·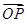 (O为坐标原点),当
(O为坐标原点),当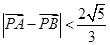 时,求实数t取值范围。
时,求实数t取值范围。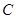 的中心在原点,焦点在
的中心在原点,焦点在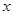 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的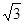 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为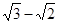
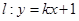 交椭圆
交椭圆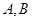 两点,当
两点,当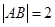 时求直线
时求直线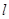 的方程
的方程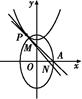
 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.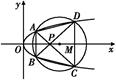
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点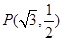 ,离心率是
,离心率是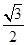 .
.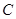 的标准方程;
的标准方程;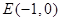 且与椭圆
且与椭圆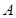 ,
,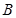 两点,若
两点,若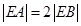 ,求直线的方程.
,求直线的方程.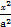 +
+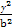 =1(a>b>0)的一个顶点A(2,0),离心率为
=1(a>b>0)的一个顶点A(2,0),离心率为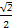 ,直线y=k(x-1)与椭圆C交于不同的两点M,N.
,直线y=k(x-1)与椭圆C交于不同的两点M,N.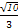 时,求k的值.
时,求k的值.