题目内容
已知椭圆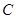 的中心在原点,焦点在
的中心在原点,焦点在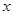 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的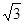 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为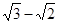
(1)求椭圆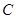 的标准方程;
的标准方程;
(2)若直线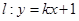 交椭圆
交椭圆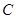 于
于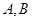 两点,当
两点,当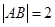 时求直线
时求直线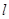 的方程
的方程
(1)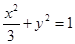 ,(2)
,(2)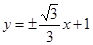
解析试题分析:(1)求椭圆标准方程,关键确定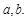 需要两个独立条件,一是长轴长是短轴长的
需要两个独立条件,一是长轴长是短轴长的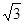 倍,故
倍,故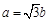 ,二是根据椭圆右顶点到右焦点的距离最短,得
,二是根据椭圆右顶点到右焦点的距离最短,得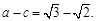 这一结论可由椭圆统一定义得到,即
这一结论可由椭圆统一定义得到,即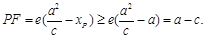 (2)由直线方程与椭圆方程联立方程组消去
(2)由直线方程与椭圆方程联立方程组消去 得
得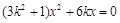 ,解得
,解得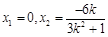 ,结合弦长公式得
,结合弦长公式得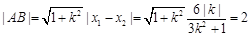 ,解得
,解得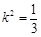 ,从而解出直线
,从而解出直线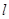 的方程
的方程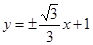 .
.
试题解析:解:(1)由题可知: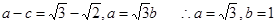
所以椭圆方程为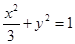 5分
5分
(2)由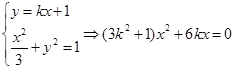
设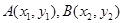 ,则
,则
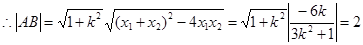 9分
9分 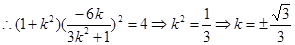
所以直线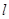 的方程为:
的方程为: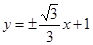 12分
12分
考点:椭圆标准方程,直线方程

练习册系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.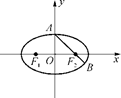
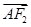 =2
=2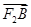 ,
,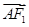 ·
· =
=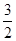 ,求椭圆的方程.
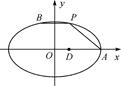
,求椭圆的方程.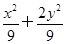 =1的右顶点,点D(1,0),点P、B在椭圆上,
=1的右顶点,点D(1,0),点P、B在椭圆上,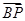 =
=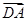 .
.
 +
+ =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
 ,
, b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0, b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程. ,
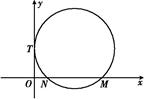
, ).
).
 +
+ =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P( ,
, ).
).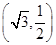 ,离心率是
,离心率是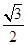 .
.