题目内容
已知△ABC中,acosA=bcosB,试判断△ABC的形状。
解:∵acosA=bcosB,
由正弦定理得sinAcosA=sinBcosB,
即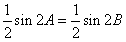 ,
,
∴2A=2B或2A+2B=π,
∴A=B或A+B= ,
,
∴△ABC为等腰三角形或直角三角形。
由正弦定理得sinAcosA=sinBcosB,
即
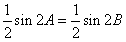 ,
,∴2A=2B或2A+2B=π,
∴A=B或A+B=
 ,
, ∴△ABC为等腰三角形或直角三角形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
