题目内容
18.当x,y满足条件|x-1|+|y+1|<1时,变量u=$\frac{x-1}{y-2}$的取值范围是(-$\frac{1}{3}$,$\frac{1}{3}$).分析 根据分式的性质,利用直线斜率的几何意义进行求解即可.
解答 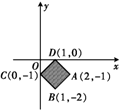 解:作出不等式|x-1|+|y+1|<1对应的区域如图:
解:作出不等式|x-1|+|y+1|<1对应的区域如图:
u=$\frac{x-1}{y-2}$=$\frac{1}{\frac{y-2}{x-1}}$,则u的几何意义表示点M(1,2)与点P(x,y)两点连线的斜率的倒数.
画出可行域如图,当点P为区域内的点(0,-1)时,umax=$\frac{1}{3}$,
当点P为区域内的点(2,-1)时,umin=$-\frac{1}{3}$,
故u的取值范围是(-$\frac{1}{3}$,$\frac{1}{3}$),
故答案为:(-$\frac{1}{3}$,$\frac{1}{3}$).
点评 本题主要考查线性规划好斜率的几何意义的应用,作出不等式组对应的平面区域是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知函数f(x)=2sin(π+x)sin(x+$\frac{π}{3}$+φ)的图象关于原点对称,其中φ∈(0,π),则函数g(x)=cos(2x-φ)的图象.( )
| A. | 关于点($\frac{π}{12},0$)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(-x)的图象向右平移$\frac{π}{12}$个单位得到 |

