题目内容
已知点A（3，4），F是抛物线y2=8x的焦点，M是抛物线上的动点，当|MA|+|MF|最小时，M点坐标是（ ）
分析：设抛物线的准线为l，过M作MB⊥l于B，过A作AC⊥l于C，利用抛物线的定义，可得结论．
解答：
解：设抛物线的准线为l，过M作MB⊥l于B，过A作AC⊥l于C，
由抛物线定义知|MF|=|MB|⇒|MA|+|MF|=|MA|+|MB|≥|AC|（折线段大于垂线段），当且仅当A，M，C三点共线取等号，即|MA|+|MF|最小．
此时M的纵坐标为4，横坐标为2
所以M（2，4）
故选C．
解：设抛物线的准线为l，过M作MB⊥l于B，过A作AC⊥l于C，由抛物线定义知|MF|=|MB|⇒|MA|+|MF|=|MA|+|MB|≥|AC|（折线段大于垂线段），当且仅当A，M，C三点共线取等号，即|MA|+|MF|最小．
此时M的纵坐标为4，横坐标为2
所以M（2，4）
故选C．
点评：本题考查抛物线的定义，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知点A（-3，-4），B（6，3）到直线l：ax+y+1=0的距离相等，则实数a的值等于（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
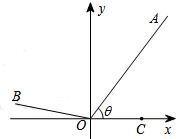如图，已知点A（3，4），C（2，0），点O为坐标原点，点B在第二象限，且|OB|=3，记∠AOC=θ．高．已知点A（3，4），B（6，m）到直线3x+4y-7=0的距离相等，则实数m等于（ ）
A、
| ||||
B、-
| ||||
| C、1 | ||||
D、
|