题目内容

19．已知f（x）=$\frac{{e}^{x}-{e}^{-x}}{2}$，g（x）=sinx，则下列函数中奇函数是①②④⑤（填写所有正确结论对应的序号）
①f（x）+g（x）；
②f（x）-g（x）；
③f（x）•g（x）；
④f（g（x））；
⑤g（f（x））．

分析 根据函数奇偶性的定义分别进判断即可．

解答 解：f（-x）=$\frac{{e}^{-x}-{e}^{x}}{2}$=-$\frac{{e}^{x}-{e}^{-x}}{2}$=-f（x），则f（x）为奇函数，
g（-x）=-sinx=-g（x），则g（x）为奇函数，
则①f（-x）+g（-x）=-[f（x）+g（x）]，则函数为奇函数；
②f（-x）-g（-x）=-[f（x）-g（x）]，则函数为奇函数；
③f（-x）•g（-x）=f（x）g（x），则函数为偶函数；
④f（g（-x））=f（-g（x））=-f（g（x）），则函数为奇函数；
⑤g（f（-x））=g（-f（x））=-g（f（x）），则函数为奇函数．
故答案为：①②④⑤．

点评 本题主要考查函数奇偶性的判断，根据奇偶性的定义是解决本题的关键．

练习册系列答案
相关题目
9．下列算法语句的处理功能是（　　）
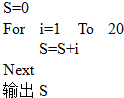
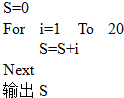
A．S=1+2+3+…+20B．S=1+2+3+…+19C．S=2+3+…+20D．S=2+3+…+19
10．已知x，y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{2y≥x-3}\end{array}\right.$，则$\frac{y}{x}$的取值范围是[-1，2]．
7．设函数f（x）=x2-klnx，k＞0．
（Ⅰ）若f（x）在点（1，f（1））处的切线过点（2，2），求k的值．
（Ⅱ）若f（x）的最小值小于零，证明f（x）在（1，$\sqrt{e}$]上仅有一个零点．
14．已知直线y=2x+1与圆x2+y2+mx=0没有公共点，则m的取值范围是（　　）
A．（4-2$\sqrt{5}$，4+2$\sqrt{5}$）B．（4-2$\sqrt{5}$，0）∪（0，4+2$\sqrt{5}$）C．（-4-2$\sqrt{5}$，-4+2$\sqrt{5}$）D．（-4-2$\sqrt{5}$，0）∪（0，-4+2$\sqrt{5}$）
4．已知函数f（x）=sin2ωx+$\sqrt{3}$sinωx•sin（ωx+$\frac{π}{2}$）（其中ω＞0）的最小正周期为$\frac{π}{2}$，
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）在区间[$\frac{π}{8}$，$\frac{π}{4}$]上的最大值与最小值．
11．某赛季，甲、乙两名篮球运动员都参加了10场比赛，比赛得分情况记录如下：
甲10304728461426114346
乙37213129193223252033
（Ⅰ）求甲10场比赛得分的中位数；
（Ⅱ）求乙10场比赛得分的方差．
8．定义：对于函数f（x），若在定义域内存在实数x0，满足f（-x0）=-f（x0），则称x0为函数f（x）的“奇对称点”．
（Ⅰ）求函数f（x）=x2+2x-4的“奇对称点”；
（Ⅱ）若函数f（x）=ln（x+m）在[-1，1]上存在“奇对称点”，求实数m的取值范围．
5．（1）求$\frac{2π}{3}$的正弦、余弦和正切值（画图）；
（2）角α的终边经过点P（-3，-4），求角α的正弦、余弦和正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网