题目内容
如图，长方体AC1中，底面ABCD为边长为2的正方形，高AA1为1，M、N分别是边C1D1与A1D1的中点．
(1)求证：四边形MNAC是等腰梯形；
(2)求梯形MNAC的面积．
答案：
解析：
提示：
解析：
|
(1)证明：连结A1C1，则MN是△A1C1D1的中位线， 于是MN ∴M、N、A、C共面，且四边形MNAC为梯形．∵Rt△AA1N≌Rt△CC1M，∴AN＝CM． ∴梯形MNAC为等腰梯形． (2)解：AN2＝A1A2＋A1N2＝1＋1＝2，AC＝ 梯形的高为h＝ ∴S梯形ACMN＝ |
A1C1．又A1C1
AC，∴MN
，MN＝
，
，
(AC＋MN)×h＝
．提示：
|
(1)要证明一个四边形是等腰梯形，应证明：①四边形是平面图形；②有一组对边平行；③另一组对边相等． (2)利用梯形面积公式，需求出上底MN、下底AC及高的长． |
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
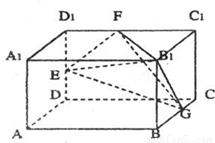
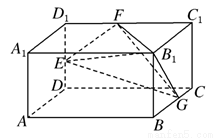
（2009•湖北模拟）如图，长方体AC1中，AB=2，BC=AA1=1，E、F、G分别为棱DD1、D1C1、BC的中点，
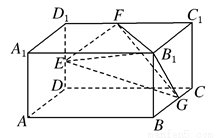
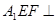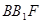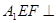平面
；
平面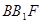
；
