题目内容
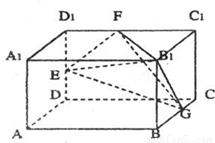
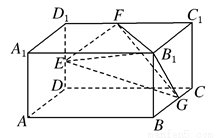
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
(1)求证:平面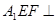 平面
平面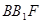 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
【答案】
(1) ,
,
 ,
, (2) 取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,∴EH∥B1G ∴EH∥平面FGB1 (3)
(2) 取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,∴EH∥B1G ∴EH∥平面FGB1 (3)
【解析】
试题分析:(1)



(2)取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,
∴EH∥B1G,又B1G?平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1= A1D1时,EH∥平面FGB1.
A1D1时,EH∥平面FGB1.
(3)∵EH∥平面FGB1,∴VE—FGB1=VH—FGB1,
而VH—FGB1=VG—HFB1= ×1×S△HFB1,
×1×S△HFB1,
S△HFB1=S梯形B1C1D1H-S△B1C1F-S△D1HF= ,
,
∴V四面体EFGB1=VE—FGB1=VH—FGB1= ×1×
×1× =
= .
.
考点:线面面面垂直平行的判定及锥体体积求解
点评:本题还可用空间向量的方法证明计算,思路简单

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 (2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,
(2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,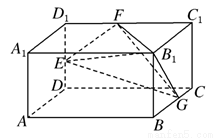
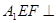 平面
平面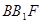 ;
;