题目内容
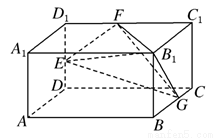
如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,(1)试在棱A1D1上找一点H,使EH∥平面FGB1;
(2)求四面体EFGB1的体积.
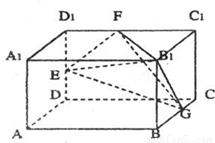
【答案】分析:(1)取A1D1的中点P,D1P的中点H,连接DP、EH,通过EH∥平面FGB1,说明EH∥B1G,得到HD1= A1D1.
A1D1.
(2)以D为原点,直线DA、DC、DD1为x、y、z轴建立空间直角坐标系,利用法向量,求出E到平面FGB1的距离d,底面 ,然后求四面体EFGB1的体积.
,然后求四面体EFGB1的体积.
解答:解:(1)取A1D1的中点P,D1P的中点H,连接DP、EH,则DP∥B1G,EH∥DP
∴EH∥B1G,又B1G?平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1= A1D1,使EH∥平面FGB1 (6分)
A1D1,使EH∥平面FGB1 (6分)
(2)以D为原点,直线DA、DC、DD1为x、y、z轴建立空间直角坐标系
则E(0,0, ),F(0,1,1),B1(1,2,1),G(
),F(0,1,1),B1(1,2,1),G( ,2,0),
,2,0),
∴ ,
, ,
, ,
,
设平面FGB1的法向量
由 得
得 ,∴x=-2,y=2,
,∴x=-2,y=2,
∵E到平面FGB1的距离d= =
=
 ,
, ,
, ,
,
∵ =
= ,
,
∴sin∠FB1G= .
.
∴ .
.
 (12分)
(12分)
点评:本题是中档题,考查直线与平面的位置关系,探究点的位置,几何体的体积的求法,考查空间想象能力,计算能力.
 A1D1.
A1D1.(2)以D为原点,直线DA、DC、DD1为x、y、z轴建立空间直角坐标系,利用法向量,求出E到平面FGB1的距离d,底面
 ,然后求四面体EFGB1的体积.
,然后求四面体EFGB1的体积.解答:解:(1)取A1D1的中点P,D1P的中点H,连接DP、EH,则DP∥B1G,EH∥DP
∴EH∥B1G,又B1G?平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1=
 A1D1,使EH∥平面FGB1 (6分)
A1D1,使EH∥平面FGB1 (6分)(2)以D为原点,直线DA、DC、DD1为x、y、z轴建立空间直角坐标系
则E(0,0,
 ),F(0,1,1),B1(1,2,1),G(
),F(0,1,1),B1(1,2,1),G( ,2,0),
,2,0),∴
 ,
, ,
, ,
,设平面FGB1的法向量

由
 得
得 ,∴x=-2,y=2,
,∴x=-2,y=2,
∵E到平面FGB1的距离d=
 =
=
 ,
, ,
, ,
,∵
 =
= ,
,∴sin∠FB1G=
 .
.∴
 .
. (12分)
(12分)点评:本题是中档题,考查直线与平面的位置关系,探究点的位置,几何体的体积的求法,考查空间想象能力,计算能力.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 (2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,
(2009•湖北模拟)如图,长方体AC1中,AB=2,BC=AA1=1,E、F、G分别为棱DD1、D1C1、BC的中点,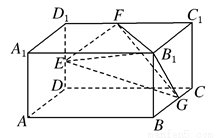
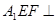 平面
平面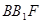 ;
;
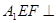 平面
平面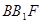 ;
;