题目内容
14.已知函数f(x)=x2+2ax+2,x∈[-5,5].(1)当a=-1时,求函数f(x)的单调递增区间;
(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.
分析 (1)将a=-1的值代入函数的解析式,求出函数的对称轴,从而求出函数的单调区间;
(2)先求出函数的对称轴,通过讨论a的范围,得到函数的单调性,进而求出满足条件的a的范围.
解答 解:(1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,
图象是抛物线,且开口向上,对称轴是x=1,
所以,当x∈[-5,5]时,f(x)的单调递减区间是[-5,1],单调递增区间是[1,5];
(2)∵f(x)=x2+2ax+2,图象是抛物线,且开口向上,对称轴是x=-a;
当x∈[-5,5]时,若-a≤-5,即a≥5时,f(x)单调递增;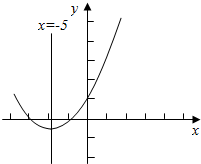
若-a≥5,即a≤-5时,f(x)单调递减;
所以,f(x)在[-5,5]上是单调函数时,
a的取值范围是(-∞,-5]∪[5,+∞).
点评 本题考查了二次函数的性质,考查函数的单调性问题,熟练掌握函数的性质是解题的关键,本题是一道中档题

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
5.函数f(x)=x2-4xsin$\frac{πx}{2}$+1(x∈R))零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.设集合A={-2,-1,0,1,2},B={x|y=log(x-3)•(1-x)},则A∩B等于( )
| A. | {2} | B. | {1,2} | C. | {0,-1,1} | D. | {-1,1} |
19.函数f(x)=(x-$\frac{1}{2}$)0+$\sqrt{x+2}$的定义域为( )
| A. | $(-2,\frac{1}{2})$ | B. | [-2,+∞) | C. | $[-2,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(\frac{1}{2},+∞)$ |