题目内容
4.在空间直角坐标系中,已知正四面体A-BCD的顶点A(0,0,0),B(0,2,0),$C({\sqrt{3},1,0})$,则顶点D的坐标为$(\frac{\sqrt{3}}{3},1,±\frac{2\sqrt{6}}{3})$.分析 由A(0,0,0),B(0,2,0),$C({\sqrt{3},1,0})$,可得|AB|=|BC|=|AC|=2,△ABC的重心G$(\frac{\sqrt{3}}{3},1,0)$.设E为边长BC的中点.可得DE=AE=$\sqrt{3}$,GE=$\frac{1}{3}AE$,设D$(\frac{\sqrt{3}}{3},1,z)$.利用DG2+GE2=DE2,即可得出.
解答 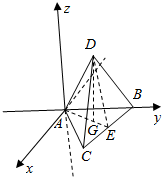 解:由A(0,0,0),B(0,2,0),$C({\sqrt{3},1,0})$,
解:由A(0,0,0),B(0,2,0),$C({\sqrt{3},1,0})$,
可得|AB|=|BC|=|AC|=2,△ABC的重心G$(\frac{\sqrt{3}}{3},1,0)$.
设E为边长BC的中点.
则DE=AE=$\sqrt{3}$,GE=$\frac{1}{3}AE$=$\frac{\sqrt{3}}{3}$,
设D$(\frac{\sqrt{3}}{3},1,z)$.
则DG2+GE2=DE2,
∴${z}^{2}+(\frac{1}{3}×\sqrt{3})^{2}$=$(\sqrt{3})^{2}$,
解得z=$±\frac{2\sqrt{6}}{3}$.
故答案为:$(\frac{\sqrt{3}}{3},1,±\frac{2\sqrt{6}}{3})$.
点评 本题考查了三角形的重心公式、正四面体的性质、勾股定理、等边三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
18.给出下列函数:①y=x3+1②y=lg$\frac{1+x}{1-x}$③y=x$+\frac{2}{x}$④y=ln($\sqrt{{x}^{2}+1}-x$),其中奇函数的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.在△ABC中,$B=\frac{π}{4},AB=\sqrt{2},BC=3$,则sinC=( )
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
13.数列{an}满足an+1=$\frac{1}{1-a_n}$,a1=$\frac{1}{2}$,则a3=( )
| A. | 1 | B. | 2 | C. | -1 | D. | $\frac{1}{2}$ |
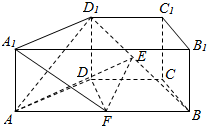 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.