题目内容
已知向量 =
= ,
, =(1,t),若函数f(x)=
=(1,t),若函数f(x)= •
• 在区间
在区间 上存在增区间,则t的取值范围________.
上存在增区间,则t的取值范围________.

分析:函数f(x)=
 •
• 在区间
在区间 上存在增区间,转化为函数的导数在区间上有大于0的区间,通过函数的最大值求解t的范围.
上存在增区间,转化为函数的导数在区间上有大于0的区间,通过函数的最大值求解t的范围.解答:函数f(x)=
 •
• =
= ,函数f(x)=
,函数f(x)= •
• 在区间
在区间 上存在增区间,
上存在增区间,所以函数f′(x)=
 -t,在区间
-t,在区间 上有
上有 -t>0成立的区间,
-t>0成立的区间,即t
 ,∵x
,∵x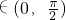 ,∴sinx<1,
,∴sinx<1,
t
 .
.故答案为:
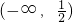
点评:本题考查向量的数量积,函数的导数的应用,考查转化思想计算能力.

练习册系列答案
相关题目