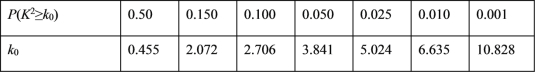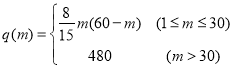题目内容
【题目】已知椭圆C:![]() 的长轴是短轴的两倍,点
的长轴是短轴的两倍,点![]() 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好构成等比数列.
恰好构成等比数列.
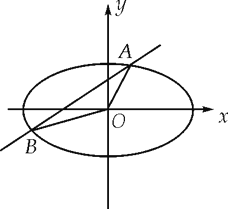
(Ⅰ)求椭圆C的方程.
(Ⅱ)试探究![]() 是否为定值?若是,求出这个值;否 则求出它的取值范围.
是否为定值?若是,求出这个值;否 则求出它的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)5.
(Ⅱ)5.
【解析】
试题(Ⅰ)求椭圆标准方程,一般利用待定系数法,只需列出两个独立条件解方程组即可;(Ⅱ)研究解析几何中定值问题,一般利用坐标运算(即解析法).先将条件![]() 、
、![]() 、
、![]() 构成等比数列转化为坐标:设
构成等比数列转化为坐标:设![]() ,则
,则![]() =
=![]() ,再利用直线方程与椭圆方程联立,结合韦达定理得
,再利用直线方程与椭圆方程联立,结合韦达定理得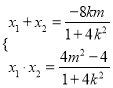 ,两者结合化简得:
,两者结合化简得:![]() ,
,![]() ,最后将
,最后将![]() 也用坐标表示并代入化简为:
也用坐标表示并代入化简为:![]() =
=![]()
=![]()
试题解析:解:(Ⅰ)由题意可知![]() 且
且![]()
![]() ,a=2
,a=2
所以椭圆的方程为![]()
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,![]()
由![]()
![]()
![]()
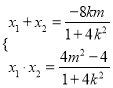 且
且![]()
![]() 恰好构成等比数列.
恰好构成等比数列.![]() =
=![]()
即![]()
![]()
![]()
因为![]() ,
,![]()
![]()
![]()
此时![]() ,即
,即![]()
![]()
故![]() =
=![]() =
=![]()
所以![]() 是定值为5.
是定值为5.

练习册系列答案
相关题目