题目内容
椭圆中心在原点,焦点在x轴上,e=
解:∵e=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴![]() =
=![]() .故可设椭圆方程为
.故可设椭圆方程为![]() +
+![]() =1.
=1.
由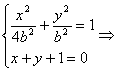 5x2+8x+4-4b2=0.
5x2+8x+4-4b2=0.
∴x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
∴y1·y2=(1+x1)(1+x2)=1+x1x2+x1+x2=![]() .
.
∵以PQ为直径的圆过原点,∴PO⊥OQ.设P(x1,y1)、Q(x2,y2),
则有x1x2+y1y2=0![]()
![]() +
+![]() =0
=0![]() b2=
b2=![]() .∴a2=
.∴a2=![]() .
.
故椭圆方程为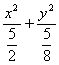 =1.
=1.

练习册系列答案
相关题目
题目内容
椭圆中心在原点,焦点在x轴上,e=
解:∵e=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴![]() =
=![]() .故可设椭圆方程为
.故可设椭圆方程为![]() +
+![]() =1.
=1.
由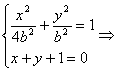 5x2+8x+4-4b2=0.
5x2+8x+4-4b2=0.
∴x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
∴y1·y2=(1+x1)(1+x2)=1+x1x2+x1+x2=![]() .
.
∵以PQ为直径的圆过原点,∴PO⊥OQ.设P(x1,y1)、Q(x2,y2),
则有x1x2+y1y2=0![]()
![]() +
+![]() =0
=0![]() b2=
b2=![]() .∴a2=
.∴a2=![]() .
.
故椭圆方程为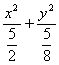 =1.
=1.
