题目内容
设向量
=(
sinx,sinx),
=(cosx,sinx),x∈[0,
]
(1)若|
|=|
|,求x的值
(2)设函数f(x)=
•
,求f(x)的取值范围.
| a |
| 3 |
| b |
| π |
| 2 |
(1)若|
| a |
| b |
(2)设函数f(x)=
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)根据|
|=|
|,就能得到关于x的方程,解方程即可.
(2)根据向量积的坐标运算求得f(x)=
sinxcosx+sin2x,根据二倍角公式,两角差的正弦公式化简f(x)=sin(2x-
)+
,根据x的取值,从而求出f(x)的取值范围.
| a |
| b |
(2)根据向量积的坐标运算求得f(x)=
| 3 |
| π |
| 6 |
| 1 |
| 2 |
解答:
解:(1)由|
|=|
|得:3sin2x+sin2x=cos2x+sin2x=1;
∴sin2x=
,∵x∈[0,
],∴sinx=
,∴x=
.
(2)f(x)=
sinxcosx+sin2x=
sin2x-
cos2x+
=sin(2x-
)+
,
∵x∈[0,
],∴2x-
∈[-
,
];
∴sin(-
)≤sin(2x-
)≤sin
∴0≤f(x)≤
;
∴f(x)的取值范围是[0,
].
| a |
| b |
∴sin2x=
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(2)f(x)=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∵x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(-
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴0≤f(x)≤
| 3 |
| 2 |
∴f(x)的取值范围是[0,
| 3 |
| 2 |
点评:熟练掌握二倍角的正余弦公式,两角差的正弦公式是求解本题的关键.

练习册系列答案
相关题目
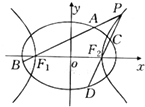 如图,已知以F1(-2,0),F2(2,0)为焦点的椭圆上有点Q,三角形QF1F2的周长为4(
如图,已知以F1(-2,0),F2(2,0)为焦点的椭圆上有点Q,三角形QF1F2的周长为4(