题目内容
已知向量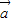 =(1,1+sinθ),
=(1,1+sinθ),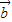 =(1,cosθ),
=(1,cosθ),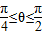 ,则
,则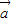 •
•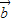 的取值范围是 .
的取值范围是 .
【答案】分析:用向量的坐标表示数量积,得到关于θ的三角函数,求导函数分析函数的单调性,运用函数单调性求值域.
解答:解:由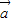 =(1,1+sinθ),
=(1,1+sinθ),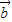 =(1,cosθ),
=(1,cosθ),
∴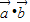 =1+cosθ+sinθcosθ,
=1+cosθ+sinθcosθ,
令f(θ)=1+cosθ+sinθcosθ,
f′(θ)=-sinθ+cos2θ-sin2θ=-2sin2θ-sinθ+1,
∵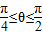 ,∴sinθ
,∴sinθ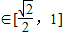 ,f′(θ)=-2sin2θ-sinθ+1<0,
,f′(θ)=-2sin2θ-sinθ+1<0,
∴f(θ)=1+cosθ+sinθcosθ在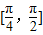 上为减函数,
上为减函数,
∴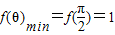 ,
,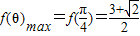 ,
,
所以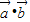 的取值范围是
的取值范围是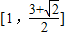 .
.
故答案为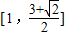
点评:本题考查了平面向量数量积的运算,考查了利用函数导函数判断函数的单调性,导函数在区间上为正,原函数在相应区间上是增函数,导函数是负,原函数是减函数,此题是中档题.
解答:解:由
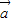 =(1,1+sinθ),
=(1,1+sinθ),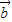 =(1,cosθ),
=(1,cosθ),∴
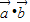 =1+cosθ+sinθcosθ,
=1+cosθ+sinθcosθ,令f(θ)=1+cosθ+sinθcosθ,
f′(θ)=-sinθ+cos2θ-sin2θ=-2sin2θ-sinθ+1,
∵
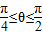 ,∴sinθ
,∴sinθ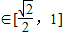 ,f′(θ)=-2sin2θ-sinθ+1<0,
,f′(θ)=-2sin2θ-sinθ+1<0,∴f(θ)=1+cosθ+sinθcosθ在
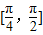 上为减函数,
上为减函数,∴
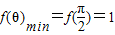 ,
,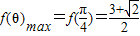 ,
,所以
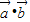 的取值范围是
的取值范围是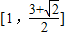 .
.故答案为
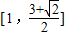
点评:本题考查了平面向量数量积的运算,考查了利用函数导函数判断函数的单调性,导函数在区间上为正,原函数在相应区间上是增函数,导函数是负,原函数是减函数,此题是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目