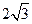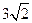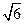题目内容
(本小题满分10分)如图,四棱锥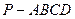 的底面ABCD是正方形,
的底面ABCD是正方形,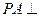 底面ABCD,E,F分别是AC,PB的中点.
底面ABCD,E,F分别是AC,PB的中点.
(I)证明: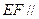 平面PCD;
平面PCD;
(Ⅱ) 若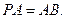 求EF与平面PAC所成角的大小.
求EF与平面PAC所成角的大小.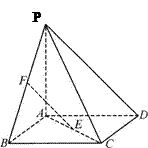
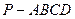 的底面ABCD是正方形,
的底面ABCD是正方形,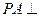 底面ABCD,E,F分别是AC,PB的中点.
底面ABCD,E,F分别是AC,PB的中点.(I)证明:
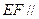 平面PCD;
平面PCD;(Ⅱ) 若
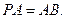 求EF与平面PAC所成角的大小.
求EF与平面PAC所成角的大小.
(I)略
(Ⅱ) EF与平面PAC所成角的大小是30°
(Ⅱ) EF与平面PAC所成角的大小是30°
(I)证明:如图,连结BD,则E是BD的中点.
又F是PB的中点,所以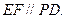
因为EF不在平面PCD内,所以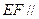 平面PCD.
平面PCD.
(Ⅱ) 解:连结PE.
因为ABCD是正方形,
所以BD^AC.又PA^平面ABC,所以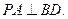
因此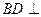 平面PAC.故
平面PAC.故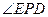 是PD与平面PAC所成的角.
是PD与平面PAC所成的角.
因为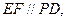 所以EF与平面PAC所成角的大小等于
所以EF与平面PAC所成角的大小等于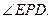
因为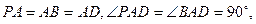 所以
所以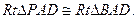
因此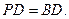 在
在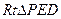 中,
中,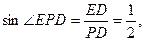

所以EF与平面PAC所成角的大小是30°
又F是PB的中点,所以
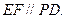
因为EF不在平面PCD内,所以
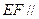 平面PCD.
平面PCD.(Ⅱ) 解:连结PE.
因为ABCD是正方形,
所以BD^AC.又PA^平面ABC,所以
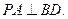
因此
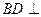 平面PAC.故
平面PAC.故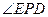 是PD与平面PAC所成的角.
是PD与平面PAC所成的角.因为
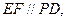 所以EF与平面PAC所成角的大小等于
所以EF与平面PAC所成角的大小等于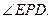
因为
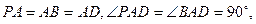 所以
所以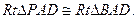
因此
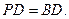 在
在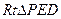 中,
中,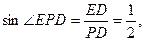

所以EF与平面PAC所成角的大小是30°

练习册系列答案
相关题目

 ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=
ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=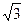 ,D是线段A1B1的中点.
,D是线段A1B1的中点.  ⊥平面A1B1BA;
⊥平面A1B1BA; ;
;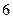 的正方体
的正方体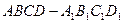 中,
中,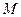 是
是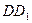 的中点,
的中点,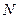 在线段
在线段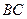 上,且
上,且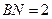 .
.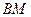 与
与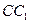 所成角的余弦值;
所成角的余弦值;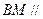 面
面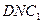 ;
;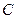 到面
到面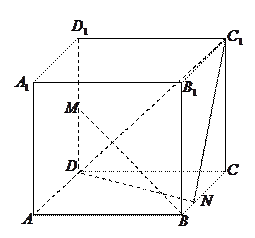
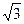 .
.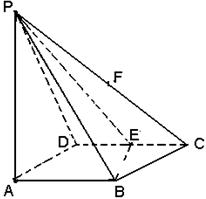
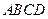 为矩形,
为矩形,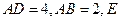 、
、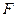 分别是线段
分别是线段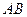 、
、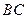 的中点,
的中点,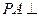 平面
平面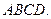 (1)求证:
(1)求证: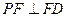 ;
; 在
在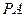 上,且
上,且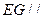 平面
平面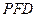 ,试确定点
,试确定点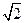 .
.
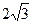 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.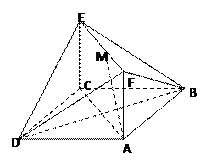
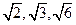 ,则对角线长为( )
,则对角线长为( )