题目内容
求函数f(x)=
解:由(sinx+cosx)2=1+2sinxcosx,
∴sinxcosx=![]() .
.
∴f(x)=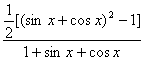
=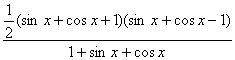
=![]() (sinx+cosx-1)(其中sinx+cosx+1≠0).
(sinx+cosx-1)(其中sinx+cosx+1≠0).
又sinx+cosx=![]() (
(![]() sinx+
sinx+![]() cosx)=
cosx)=![]() sin(x+
sin(x+![]() ),
),
∴sinx+cosx∈[-![]() ,
,![]() ],且sinx+cosx≠-1.
],且sinx+cosx≠-1.
∴f(x)的值域为[![]() ,-1)∪(-1,
,-1)∪(-1,![]() ].
].

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
求函数f(x)=
解:由(sinx+cosx)2=1+2sinxcosx,
∴sinxcosx=![]() .
.
∴f(x)=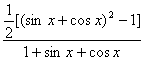
=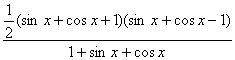
=![]() (sinx+cosx-1)(其中sinx+cosx+1≠0).
(sinx+cosx-1)(其中sinx+cosx+1≠0).
又sinx+cosx=![]() (
(![]() sinx+
sinx+![]() cosx)=
cosx)=![]() sin(x+
sin(x+![]() ),
),
∴sinx+cosx∈[-![]() ,
,![]() ],且sinx+cosx≠-1.
],且sinx+cosx≠-1.
∴f(x)的值域为[![]() ,-1)∪(-1,
,-1)∪(-1,![]() ].
].

 名校课堂系列答案
名校课堂系列答案