题目内容
在△ABC中,满足 与
与 的夹角为60°,M是AB的中点.
的夹角为60°,M是AB的中点.
(1)若| |=|
|=| |,求向量
|,求向量 与
与 的夹角的余弦值.
的夹角的余弦值.
(2)若|AB|=2,| |=2
|=2 ,在AC上确定一点D的位置,使得
,在AC上确定一点D的位置,使得 达到最小,并求出最小值.
达到最小,并求出最小值.
解:(1)设| |=|
|=| |=a,cos<
|=a,cos< ,
, >=
>= =
=
(2)因为 ,|AB|=2,|
,|AB|=2,| |=2
|=2 ,由余弦定理知:|AC|=4
,由余弦定理知:|AC|=4
M是AB的中点,所以AM=1,因为D是AC上一点,设AD=x,则DC=4-x,所以
 =
=
=
所以当x= 时,即D距A点
时,即D距A点 处,
处, 取到最小,最小值为
取到最小,最小值为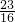 .
.
分析:(1)设| |=|
|=| |=a,根据数量积的运算求余弦值,
|=a,根据数量积的运算求余弦值,
(2)根据余弦定理求出|AC|=4,则AM=1,设AD=x,则DC=4-x,用x表示出 ,根据一元二次函数求最值的方法求出最值.
,根据一元二次函数求最值的方法求出最值.
点评:本题考查了平面向量数量积的运算,以及一元二次函数求最值,是综合题.
 |=|
|=| |=a,cos<
|=a,cos< ,
, >=
>= =
=
(2)因为
 ,|AB|=2,|
,|AB|=2,| |=2
|=2 ,由余弦定理知:|AC|=4
,由余弦定理知:|AC|=4M是AB的中点,所以AM=1,因为D是AC上一点,设AD=x,则DC=4-x,所以
 =
=
=

所以当x=
 时,即D距A点
时,即D距A点 处,
处, 取到最小,最小值为
取到最小,最小值为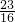 .
.分析:(1)设|
 |=|
|=| |=a,根据数量积的运算求余弦值,
|=a,根据数量积的运算求余弦值,(2)根据余弦定理求出|AC|=4,则AM=1,设AD=x,则DC=4-x,用x表示出
 ,根据一元二次函数求最值的方法求出最值.
,根据一元二次函数求最值的方法求出最值.点评:本题考查了平面向量数量积的运算,以及一元二次函数求最值,是综合题.

练习册系列答案
相关题目
 与
与 的夹角为60°,M是AB的中点.
的夹角为60°,M是AB的中点. |=|
|=| |,求向量
|,求向量 与
与 的夹角的余弦值.
的夹角的余弦值. |=2
|=2 ,在AC上确定一点D的位置,使得
,在AC上确定一点D的位置,使得 达到最小,并求出最小值.
达到最小,并求出最小值. 与
与 的夹角为60°,M是AB的中点.
的夹角为60°,M是AB的中点. |=|
|=| |,求向量
|,求向量 与
与 的夹角的余弦值.
的夹角的余弦值. |=2
|=2 ,在AC上确定一点D的位置,使得
,在AC上确定一点D的位置,使得 达到最小,并求出最小值.
达到最小,并求出最小值.