Question

已知抛物线y²=2px（p＞0）的焦点为F，准线为L，点M在L上，且线段MF交抛物线于点N，若|MN|=2|NF|，且△OMN（O是坐标原点）的面积为

2

3

3

，则p=

 

．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：根据抛物线的定义，得到三角形的面积关系即可得到结论．

解答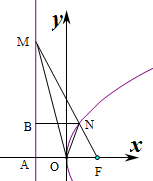： 解：过N作NB⊥l于B，则|NF|=|NB|，
若|MN|=2|NF|，
则|MN|=2|NF|=2|NB|，
即

|BN|

|MN|

=

1

2

，
则∠AMF=30°，
∵|AF|=p，∴|MF|=2p，|AM|=

3

p，
|MN|=

2

3

×2p=

4p

3

，|MB|=|MN|cos30°=

4p

3

×

3

2

=

2 3 p

3

，
则|AB|=|AM|-|MB|=

3

p-

2 3 p

3

=

3 p

3

，
则S_△OMN=S_△AMF-S_△AOM-S_△ONF=

1

2

×p×

3

p-

1

2

×

p

2

×

3

p-

1

2

×

p

2

×

3 p

3

=

3 p2

6

=

2

3

3

，
即p²=4，解得p=2，
故答案为：2

点评：本题主要考查抛物线的方程的应用，根据抛物线的定义建立条件关系是解决本题的关键．