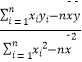题目内容
【题目】已知向量 
=（1+sin2x，sinx﹣cosx）， 
=（1，sinx+cosx），函数f（x）= 
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的最大值及取得最大值相应的x的集合．
【答案】
（1）解：f（x）= 
=（1+sin2x）+（sin2x﹣cos2x）
=1+sin2x﹣（cos2x﹣sin2x）
=1+sin2x﹣cos2x
= 
；
f（x）的最小正周期为 
（2）解：当sin（2x﹣ 
）=1时，f（x）取得最大值为 
；
由 
，得 
，
即 
；
所以f（x）取得最大值时x的集合为 
【解析】（1）利用平面向量数量积的坐标运算化简函数f（x），结合三角恒等变换即可求出f（x）的最小正周期，（2）利用正弦函数的图象与性质即可求出f（x）的最大值及取得最大值相应的x的集合．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
