题目内容
对于函数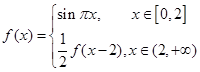 ,有下列4个命题:
,有下列4个命题:
①任取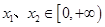 ,都有
,都有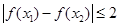 恒成立;
恒成立;
②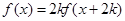
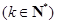 ,对于一切
,对于一切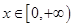 恒成立;
恒成立;
③函数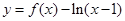 有3个零点;
有3个零点;
④对任意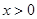 ,不等式
,不等式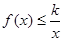 恒成立,则实数
恒成立,则实数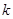 的取值范围是
的取值范围是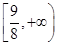 .
.
则其中所有真命题的序号是 .
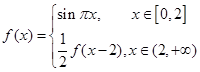 ,有下列4个命题:
,有下列4个命题:①任取
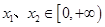 ,都有
,都有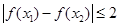 恒成立;
恒成立;②
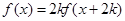
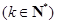 ,对于一切
,对于一切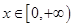 恒成立;
恒成立;③函数
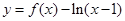 有3个零点;
有3个零点;④对任意
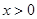 ,不等式
,不等式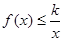 恒成立,则实数
恒成立,则实数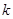 的取值范围是
的取值范围是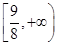 .
.则其中所有真命题的序号是 .
①③
试题分析:从函数的定义可知
 ,
, ,因此
,因此 ,①正确;由定义
,①正确;由定义
 ,因此
,因此 ,②错误;函数
,②错误;函数 与
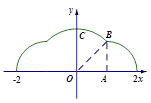
与 的图象如下图所求,它们有三个交点,因此方程
的图象如下图所求,它们有三个交点,因此方程 有3个解,③正确;对④,由于
有3个解,③正确;对④,由于 ,
, ,即
,即 时,不等式
时,不等式 不恒成立,故④错误.(事实上从函数定义或图象可知
不恒成立,故④错误.(事实上从函数定义或图象可知

 ,因此不等式
,因此不等式 要成立,必须有
要成立,必须有 ,
, ,而当
,而当 时,
时, 的最大值为
的最大值为 (
( 时取得),故
时取得),故 .),故填①③.
.),故填①③.

练习册系列答案
相关题目
 ,
,
 ,函数
,函数 的图像与直线
的图像与直线 的相邻两个交点之间的距离为
的相邻两个交点之间的距离为 .
. 的值;
的值; 在
在 上的单调递增区间.
上的单调递增区间.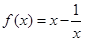 .
.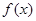 的奇偶性,并加以证明;
的奇偶性,并加以证明;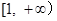 上为增函数;
上为增函数;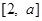 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于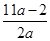 ,求
,求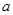 的取值范围.
的取值范围.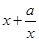 ,x∈
,x∈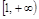 ,
,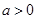 .
.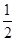 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;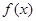 的最小值为4,求实数
的最小值为4,求实数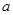
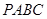 沿
沿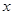 轴滚动,点
轴滚动,点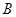 恰好经过原点.设顶点
恰好经过原点.设顶点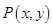 的轨迹方程是
的轨迹方程是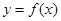 ,则对函数
,则对函数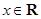 ,都有
,都有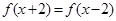 ;③函数
;③函数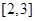 上单调递减;④函数
上单调递减;④函数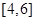 上是减函数.其中判断正确的序号是 .
上是减函数.其中判断正确的序号是 .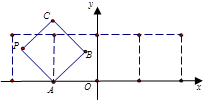
 .若
.若 ,则( )
,则( )










 |)<f(1)的实数x的取值范围是( )
|)<f(1)的实数x的取值范围是( )