Question

已知点P为椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)上一动点，椭圆C左，右顶点分别为A，B，左焦点为F，若|PF|最大值与最小值分别为4和2．
（1）求椭圆C的标准方程；
（2）已知直线l过点A且倾斜角为30°，点M为椭圆C长轴上一动点，且点M到直线l的距离等于|MB|，若连接PM并延长与椭圆C交于点Q，求S_△APQ的最大值．

Answer 1

分析：（1）设c是此椭圆的半焦距，由于|PF|最大值与最小值分别为4和2，可得

a+c=4 a-c=2

，解出即可；
（2）由（1）可知A（-3，0），B（3，0）．又k=tan30°=

3

3

．可得直线l的方程为y=

3

3

(x+3)，设M（m，0），（-3≤m≤3），利用点到直线的距离公式可得点M到直线l的距离d，又|BM|=3-m，d=|MB|，解得m=1．M（1，0）．设直线PQ的方程为：my=x-1，P（x₁，y₁），Q（x₂，y₂）．与椭圆的方程联立即可得到根与系数的关系，利用点到直线的距离公式可得点A到直线l的距离d₁，利用弦长公式可得|PQ|，即可得到S_△APQ=

1

2

d1|PQ|，再利用导数研究其单调性最值即可得出．

解答：解：（1）设c是此椭圆的半焦距，∵|PF|最大值与最小值分别为4和2，
∴

a+c=4 a-c=2

，解得a=3，c=1，
∴b²=a²-c²=8．
∴椭圆C的标准方程是

x2

9

+

y2

8

=1．
（2）如图所示，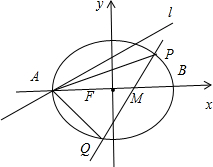
由（1）可知A（-3，0），B（3，0）．
又k=tan30°=

3

3

．
∴直线l的方程为y=

3

3

(x+3)，化为x-

3

y+3=0．
设M（m，0），（-3≤m≤3），则点M到直线l的距离d=

|m+3|

1+( 3 )2

=

3+m

2

，
又|BM|=3-m，d=|MB|，∴

3+m

2

=3-m，解得m=1．∴M（1，0）．
设直线PQ的方程为：my=x-1，P（x₁，y₁），Q（x₂，y₂）．
联立

my=x-1 x2 9 + y2 8 =1

，化为（8m²+9）y²+16my-64=0，
显然△＞0．
∴y1+y2=-

16m

8m2+9

，y1y2=

-64

8m2+9

．
∴|PQ|=

(1+m2)[(y1+y2)2-4y1y2]

=

(1+m2)[( 16m 8m2+9 )2+ 4×64 8m2+9 ]

=

48(1+m2)

8m2+9

．
点A到直线l的距离d=

4

1+m2

．
∴S_△APQ=

1

2

d|PQ|=

1

2

×

4

1+m2

×

48(1+m2)

8m2+9

=

96 1+m2

8m2+9

．
令

1+m2

=t≥1，g（t）=S（m）=

96t

8t2+1

．
g′(t)=

96(1-8t2)

(8t2+1)2

＜0，因此g（t）在[1，+∞）上单调递减，
∴S（m）=g（t）≤g（1）=

96

8+1

=

32

3

．当且仅当m=0即PQ⊥x轴时取等号．
∴当PQ⊥x轴时，S_△APQ的最大值为

32

3

．

点评：本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、点到直线的距离公式、弦长公式、三角形的面积公式、利用导数研究函数的单调性等基础知识与基本技能方法，属于难题．