题目内容
(本小题满分15分)已知数列 的前
的前 项和
项和 满足:
满足: (
( 为常数,且
为常数,且 ).
).
(1)设 ,若数列
,若数列 为等比数列,求
为等比数列,求 的值;
的值;
(2)在满足条件(1)的情形下,设 ,数列
,数列 的前
的前 项和为
项和为 ,若不等式
,若不等式
 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ,(2)
,(2)
【解析】
试题分析:(1)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与 的关系,再求
的关系,再求 ;(2)对于恒成立的问题,常用到以下两个结论:
;(2)对于恒成立的问题,常用到以下两个结论:
(1) ,(2)
,(2)
试题解析:当 时,
时, ,得
,得 .
.
当 时,由
时,由 ,即
,即 ,①
,①
得, ,②
,②
 ,即
,即 ,
,
 是等比数列,且公比是
是等比数列,且公比是 ,
, . (3分)
. (3分)
(1) ,即
,即 ,
,
若数列 为等比数列,则有
为等比数列,则有 ,
,
而 ,
,
故 ,解得
,解得 ,
,
再将 代入
代入 ,得
,得 ,
,
由 ,知
,知 为等比数列,
为等比数列, . (5分)
. (5分)
(2)由 ,知
,知 ,
, ,
,
 ,
,
由不等式 恒成立,得
恒成立,得 恒成立,设
恒成立,设 ,由
,由
 ,
,
 当
当 时,
时, ,当
,当 时,
时, ,
,
而 ,
,
 . (8分)
. (8分)
考点:等比数列的概念与求和公式、不等式等基础知识,同时考查运算求解能力。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
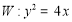 的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l:
的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l: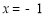 的距离为
的距离为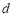 ,则有( )
,则有( )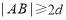 (B)
(B) (C)
(C)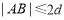 (D)
(D)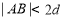
 为双曲线C:
为双曲线C: 的左、右焦点,点P为双曲线C上一点,如果
的左、右焦点,点P为双曲线C上一点,如果 ,那么双曲线C的方程为____;离心率为____.
,那么双曲线C的方程为____;离心率为____.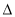 ABC中,角A,B,C所对的边分别为a,b,c. 若
ABC中,角A,B,C所对的边分别为a,b,c. 若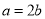 ,
,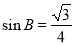 ,则( )
,则( )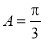 (B)
(B)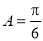
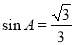 (D)
(D)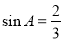
 、
、 满足
满足 且
且 的最小值为
的最小值为 ,则实数
,则实数 的值为 。
的值为 。 ,若函数
,若函数 在区间
在区间 上有三个零点,则实数
上有三个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C.  D.
D.

 共线,则t= .
共线,则t= .