题目内容
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积是( )
A.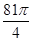 | B.16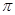 | C.9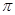 | D. |
A
试题分析:由已知条件可知球心在正四棱锥的高上,设球的半径为R,球心为O,正四棱锥底面中心为为E,则OE垂直棱锥底面,OE=4-R,所以(4-R)2+
 =R2,解得R=
=R2,解得R= ,所以球的表面积S=4
,所以球的表面积S=4 =
=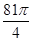 .
.【考点】正四棱锥的性质和球的表面积.

练习册系列答案
相关题目
题目内容
A.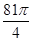 | B.16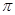 | C.9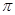 | D. |
 =R2,解得R=
=R2,解得R= ,所以球的表面积S=4
,所以球的表面积S=4 =
=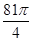 .
.