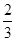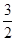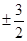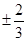题目内容
已知等比数列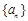 各项都是正数,
各项都是正数, ,
,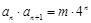 ,
,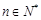 .
.
(1)求数列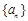 的通项公式;
的通项公式;
(2)求证: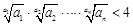 .
.
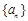 各项都是正数,
各项都是正数, ,
,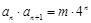 ,
,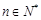 .
.(1)求数列
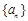 的通项公式;
的通项公式;(2)求证:
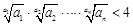 .
.(1) .(2)见解析.
.(2)见解析.
 .(2)见解析.
.(2)见解析.试题分析:(1)设
 的公比为
的公比为 ,由已知可得
,由已知可得 ,
,两式相除得:
 ,即可得到
,即可得到 ,
, .
.(2)由(1)知
 ,
,首先得到
 .
.利用“错位相减法”求得

 ,
,即得证.
试题解析:(1)设
 的公比为
的公比为 ,由已知
,由已知 ,
,两式相除得:
 ,故
,故 ,
, . 6分
. 6分(2)由(1)知
 ,
, 9分
9分设
 ,则
,则 ,两式相减得:
,两式相减得: ,
, ,
, ,即
,即 . 13分
. 13分
练习册系列答案
相关题目
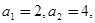 数列
数列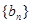 满足:
满足: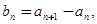
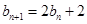 .
.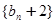 是等比数列(要指出首项与公比);
是等比数列(要指出首项与公比);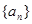 的通项公式.
的通项公式. 的前
的前 项和
项和 与
与 满足
满足 .
. 的前
的前 .
.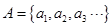 ,定义
,定义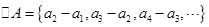 它的第
它的第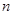 项为
项为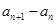
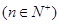 ,假设
,假设 是首项是
是首项是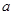 公比为
公比为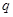 的等比数列.
的等比数列.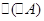 的前
的前 ;
;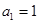 ,
,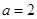 ,
,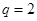 .
.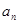 ;
;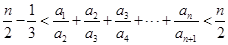 .
. 的首项
的首项 .
. 为等比数列;
为等比数列; ,若
,若 ,求最大正整数
,求最大正整数 的值;
的值; ,使
,使 成等比数列?如果存在,请给予证明;如果不存在,请说明理由.
成等比数列?如果存在,请给予证明;如果不存在,请说明理由.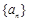 的前
的前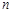 项和为
项和为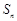 满足
满足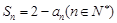 .
.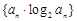 的前
的前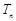 .
.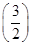 n-1
n-1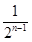
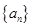 中,
中,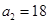 ,
,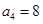 ,则数列
,则数列