题目内容

已知向量a=(sinx,cosx),b=(cosx,-cosx),f(x)=2a·b+|a|.

（1）写出函数f(x)的解析式；

（2）求f(x)的单调区间；

（3）若在［0,π］上，f(x)=m有两个不同的实根，求实数m的取值范围.

解析:（1）由条件可得a·b=sinxcosx-cos2x,|a|=1,

f(x)=2sinxcosx-2cos2x+1=sin2x-(cos2x+1)+1=sin2x-cos2x=sin(2x-).

（2）由2kπ-≤2x-≤2kπ+ (k∈Z)可得kπ-≤x≤kπ+(k∈Z),所以，f(x)的单调递增区间为［kπ-,kπ+］(k∈Z).

同理可得f(x)的单调递减区间为［kπ+,kπ+］(k∈Z).

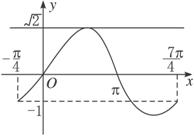
（3）令2x-=θ,由于x∈［0,π］，所以θ∈［-,］,在同一坐标系下，画出函数y=2sinθ与y=m的图象，如图根据图象可知m∈［-1,).


练习册系列答案
相关题目
已知向量
a
=(sinθ，
3
)，
b
=(1，cosθ)，θ∈(-
π
2
，
π
2
)．
（1）若
a
⊥
b
，求θ；
（2）求|
a
+
b
|的最大值．
已知向量
a
=(sin(x-
π
4
)，-1)，
b
=(
2
，2)且f(x)=
a
•
b
+2
（1）求f（x）的表达式．
（2）用“五点作图法”画出函数f（x）在一个周期上的图象．
（3）写出f（x）在[-π，π]上的单调递减区间．
（4）设关于x的方程f（x）=m在x∈[-π，π]上的根为x1，x2且m∈(1，
2
)，求x1+x2的值．
已知向量
a
=(sinθ，-2)，
b
=(1，cosθ)，且
a
⊥
b
，则sin2θ+cos2θ的值为（　　）
已知向量
a
=(sinθ，1)，
b
=(1，cosθ)，θ∈(-
π
2
，
π
2
)．
（1）若
a
⊥
b
，求θ的值；
（2）若已知sinθ+cosθ=
2
sin(θ+
π
4
)，利用此结论求|
a
+
b
|的最大值．
已知向量
a
=(sin(x-
π
4
)，-1)，
b
=(2，2)且f(x)=
a
•
b
+2
①用“五点法”作出函数y=f（x）在长度为一个周期的闭区间的图象．
②求函数f（x）的最小正周期和单调增区间；
③求函数f（x）的最大值，并求出取得最大值时自变量x的取值集合
④函数f（x）的图象可以由函数y=sin2x（x∈R）的图象经过怎样的变换得到？
⑤当x∈[0，π]，求函数y=2sin(x-
π
4
)的值域
解：（1）列表
（2）作图
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网