题目内容
已知P(1,2)为圆x2+y2=9内一定点,过P作两条互相垂直的任意弦交圆于B、C两点,求B、C中点M的轨迹方程.
答案:
解析:
提示:
解析:
|
解:设点M的坐标为(a,b),并设点B、C两点的坐标分别为(x1,y1)、(x2,y2),则由点M是B、C两点的中点,可得 由x12+y12=9,x22+y22=9,得到x12+y12+x22+y22=18,可得到(x1+x2)2+(y1+y2)2-2x1x2-2y1y2-18=0,解得x1x2+y1y2=2a2+2b2-9;① 由 将②和①联立得到2a2+2b2-9=2a+4b-5,化简即得到a2+b2-a-2b-2=0,所以点M的轨迹方程为x2+y2-x-2y-2=0. |
提示:
|
设点M的坐标为(a,b),并设点B、C两点的坐标分别为(x1,y1)、(x2,y2),然后根据 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
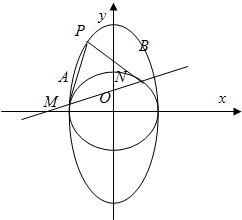 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: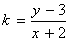 的最大值和最小值。
的最大值和最小值。