题目内容
【题目】如图,在直三棱柱![]() 中,
中, ![]() 为
为![]() 的中点,
的中点, ![]() .
.
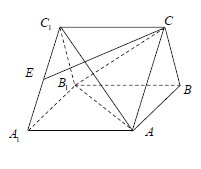
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:
(1)要证直线![]() 与平面
与平面![]() 垂直,就要证
垂直,就要证![]() 与平面
与平面![]() 内两条相交直线垂直,由已知
内两条相交直线垂直,由已知![]() ,
, ![]() 为
为![]() 中点可证
中点可证![]() ,从而可得
,从而可得![]() ,另外直三棱柱的底面是直角三角形,因此有
,另外直三棱柱的底面是直角三角形,因此有![]() 与侧面
与侧面![]() 垂直,从而得
垂直,从而得![]() ,这样由线面垂直的判定定理可得线面垂直;
,这样由线面垂直的判定定理可得线面垂直;
(2)要求![]() 到平面
到平面![]() 的距离,可用体积法求得,首先求出
的距离,可用体积法求得,首先求出![]() 的面积,通过计算求出(已知除外)三边长,另外
的面积,通过计算求出(已知除外)三边长,另外![]() 的体积可通过
的体积可通过![]() 来求,这里
来求,这里![]() 到平面
到平面![]() 的距离就是
的距离就是![]() ((1)中已证),体积可求.
((1)中已证),体积可求.
试题解析:
(1)证明:

∵直三棱柱![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 与
与![]() 相似,且有
相似,且有![]() ,
,
∵![]() ,
,
∴![]()
![]() ;
;
(2)在矩形![]() 中,
中, ![]() 为
为![]() 的中点,
的中点,
可得![]() ,
,
在![]() ,由
,由![]() 可得
可得![]() ,
,
从而可求得![]() ,
,
显然有![]() ,即
,即![]() ,
,
![]() 为点
为点![]() 到平面
到平面![]() 的距离,
的距离,
∵![]() 平面
平面![]() ,
,
由![]() ,可得
,可得![]() ,
,
计算得![]() ,
, ![]() ,
,
∴![]() ,可推出
,可推出![]() ,
,
∴点![]() 到平面
到平面![]() 的距离是
的距离是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目