题目内容
已知抛物线C:y=-| 1 | 2 |
(1)证明:直线AB的斜率为定值.(2)当直线AB在y轴上的截距为正数时,求△PAB面积的最大值及此时直线AB的方程.
分析:(1)设出A、B坐标,利用一元二次方程根与系数的关系,求出A、B横坐标之差,纵坐标之差,从而求出AB斜率.
(2)设出AB直线方程,与抛物线方程联立,运用根与系数的关系求AB长度,计算P到AB的距离,计算△PAB面积,
使用基本不等式求最大值.
(2)设出AB直线方程,与抛物线方程联立,运用根与系数的关系求AB长度,计算P到AB的距离,计算△PAB面积,
使用基本不等式求最大值.
解答:解:(Ⅰ)证:易知点P在抛物线C上,设PA的斜率为k,则直线PA的方程是y-4=k(x-2).
代入y=-
x2+6并整理得x2+2kx-4(k+1)=0此时方程应有根xA及2,
由韦达定理得:
2xA=-4(k+1),∴xA=-2(k+1).∴yA=k(xA-2)+4.=-k2-4k+4.∴A(-2(k+1),-k2-4k+4).
由于PA与PB的倾斜角互补,故PB的斜率为-k.
同理可得B(-2(-k+1),-k2+4k+4)
∴kAB=2.
(Ⅱ)∵AB的方程为y=2x+b,b>0.代入方程y=-
x2+6消去y得
x2+2x+b-6=0.
|AB|=2
=2
.
∴S=
|AB|d=
•2
•
≤
=
.
此时方程为y=2x+
.
代入y=-
| 1 |
| 2 |
由韦达定理得:
2xA=-4(k+1),∴xA=-2(k+1).∴yA=k(xA-2)+4.=-k2-4k+4.∴A(-2(k+1),-k2-4k+4).
由于PA与PB的倾斜角互补,故PB的斜率为-k.
同理可得B(-2(-k+1),-k2+4k+4)
∴kAB=2.
(Ⅱ)∵AB的方程为y=2x+b,b>0.代入方程y=-
| 1 |
| 2 |
| 1 |
| 2 |
|AB|=2
| (1+22)[4-2(b-6)] |
| 5(16-2b) |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5(16-2b) |
| b | ||
|
| (16-2b)•b•b |
(
|
64
| ||
| 9 |
此时方程为y=2x+
| 16 |
| 3 |
点评:本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力.

练习册系列答案
相关题目
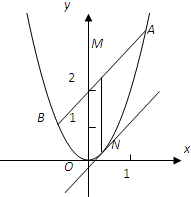 已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.