题目内容
已知抛物线C:y=
(x2+x),点A(-1,0),B(0,2),点E是曲线C上的一个动点(E不在直线AB上),设E(x0,y0),C,D在直线AB上,ED⊥AB,EC⊥x轴.
(1)用x0表示
在
方向上的投影;
(2)
2是否为定值?若是,求此定值,若不是,说明理由.
| 1 |
| 2 |
(1)用x0表示
| AE |
| AB |
(2)
|
| ||
|
|
分析:(1)根据E(x0,y0),A(-1,0),B(0,2),写出向量
、
的坐标,根据投影的定义可用x0表示
在
方向上的投影;
(2)先求出点D的坐标,进而表示出向量
,
,再求出相应的模,即可得结论.
| AE |
| AB |
| AE |
| AB |
(2)先求出点D的坐标,进而表示出向量
| AC |
| AD |
解答:解:(1)E(x0,y0),A(-1,0),B(0,2)
∴
=(x0+1,y0),
=(1,2)
∴
在
方向上的投影为
=
=
=
(2)直线AB为y=2x+2,所以C(x0,2x0+2),D(
-
,
+
)
∴
=(x0+1,2x0+2),
=(
+
,
+
)
∴
2=5
∴
| AE |
| AB |
∴
| AE |
| AB |
| ||||
|
|
| x0+1+2y0 | ||
|
x0+1+
| ||
|
| ||
|
(2)直线AB为y=2x+2,所以C(x0,2x0+2),D(
| 1 |
| 5 |
| x | 2 0 |
| 4 |
| 5 |
| 2 |
| 5 |
| x | 2 0 |
| 2 |
| 5 |
∴
| AC |
| AD |
| 1 |
| 5 |
| x | 2 0 |
| 1 |
| 5 |
| 2 |
| 5 |
| x | 2 0 |
| 2 |
| 5 |
∴
|
| ||
|
|
| 5 |
点评:本题以抛物线为载体,考查向量的数量积,考查向量的模,有一定的综合性.

练习册系列答案
相关题目
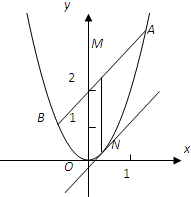 已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作轴的垂线交C于点N.