题目内容
【题目】(1)已知直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() .设
.设![]() 与圆
与圆![]() 相交与两点A,B,求点P到两点的距离之积.
相交与两点A,B,求点P到两点的距离之积.
(2)在极坐标系中,圆C的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
①若直线![]() 过圆C的圆心,求实数
过圆C的圆心,求实数![]() 的值;
的值;
②若![]() ,求直线
,求直线![]() 被圆C所截得的弦长.
被圆C所截得的弦长.
【答案】(1)2;(2)①![]() ;②
;②![]()
【解析】
(1)求出直线的参数方程,并代入圆的方程,利用直线参数方程的几何意义即可求解;
(2)将极坐标方程化为直角坐标方程,①将圆心![]() 代入直线
代入直线![]() 即可求出
即可求出
②先求出圆心到直线的距离,根据弦长公式即可得出直线![]() 被圆C所截得的弦长.
被圆C所截得的弦长.
(1)直线的参数方程为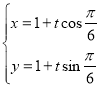 ,即
,即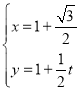 .
.
把直线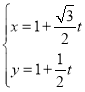 代入
代入![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,
则点P到A,B两点的距离之积为2.
(2)①以极点为坐标原点,极轴所在直线为x轴建立直角坐标系.
由![]() 得
得![]() ,
,
则圆C的直角坐标方程是![]() ,
,
圆心坐标为![]() ,半径
,半径![]() .
.
由![]() ,得
,得![]() ,
,
则直线l的直角坐标方程是![]() .
.
若直线l通过圆C的圆心,则![]() ,所以
,所以![]() .
.
②若![]() ,则圆心到直线的距离
,则圆心到直线的距离![]() ,
,
所以直线l被圆C所截得的弦长为![]() .
.

练习册系列答案
相关题目
