题目内容
对于数列 :
: ,若不改变
,若不改变 ,仅改变
,仅改变 中部分项的符号,得到的新数列
中部分项的符号,得到的新数列 称为数列
称为数列 的一个生成数列.如仅改变数列
的一个生成数列.如仅改变数列 的第二、三项的符号可以得到一个生成数列
的第二、三项的符号可以得到一个生成数列 .
.
已知数列 为数列
为数列 的生成数列,
的生成数列, 为数列
为数列 的前
的前 项和.
项和.
⑴写出 的所有可能值;
的所有可能值;
⑵若生成数列 满足:
满足:  ,求
,求 的通项公式;
的通项公式;
⑶证明:对于给定的 ,
, 的所有可能值组成的集合为:
的所有可能值组成的集合为:
 .
.
(1)由已知, ,
, ,
,
∴
由于
∴ 可能值为
可能值为 .
.
(2)∵ ,
,
当 时,
时, ,
,
当 时,
时,
∵ 是
是 的生成数列
的生成数列
∴ ;
; ;
; ;
;
∴
在以上各种组合中,
当且仅当 时,才成立。
时,才成立。
∴
(3)证法一:用数学归纳法证明:
① 时,
时,  ,命题成立。
,命题成立。
②假设 时命题成立,即
时命题成立,即 所有可能值集合为:
所有可能值集合为:

由假设, =
=
则当 ,
,


即 或
或

即
 ∴
∴ 时,命题成立
时,命题成立
由①②, ,
, 所有可能值集合为
所有可能值集合为 。
。
证法二:
 共有
共有 种情形。
种情形。

即
又 ,分子必是奇数,满足条件
,分子必是奇数,满足条件 的奇数
的奇数 共有
共有 个。
个。
设数列 与数列
与数列 为两个生成数列,数列
为两个生成数列,数列 的前
的前 项和
项和 ,数列
,数列 的前
的前 项和
项和 ,从第二项开始比较两个数列,设第一个不相等的项为第
,从第二项开始比较两个数列,设第一个不相等的项为第 项。
项。
由于 ,不妨设
,不妨设 ,则
,则


所以,只有当数列 与数列
与数列 的前
的前 项完全相同时,才有
项完全相同时,才有 。
。
∴ 共有
共有 种情形,其值各不相同。
种情形,其值各不相同。
∴ 可能值必恰为
可能值必恰为 ,共
,共 个。
个。
即 所有可能值集合为
所有可能值集合为

练习册系列答案
相关题目
 ,解关于x的不等式
,解关于x的不等式  .
. 分别是椭圆
分别是椭圆 的左、右焦点,若椭圆上存在一点
的左、右焦点,若椭圆上存在一点 ,
,  为
为 的内心,使
的内心,使 ,则该椭圆的离心率等于 .
,则该椭圆的离心率等于 . 表示不小于
表示不小于 .定义在
.定义在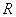 上的函数
上的函数 ,若集合
,若集合 ,则集合
,则集合 中所有元素的和为 .
中所有元素的和为 .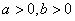 ,对于定义在
,对于定义在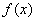 ,有下述命题:
,有下述命题: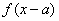 的图像关于点
的图像关于点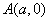 对称”;
对称”;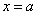 对称”;
对称”;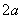 是
是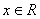 ,都有
,都有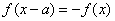 ”;
”;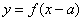 与
与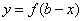 的图像关于
的图像关于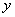 轴对称”的充要条件是“
轴对称”的充要条件是“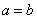 ”
” 的大小关系是( ).
的大小关系是( ). (B)
(B) 
 (D)
(D) 
 被圆
被圆 截得的弦长为__________
截得的弦长为__________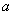 ,b,c.若
,b,c.若 ,
, ,则角
,则角 =
=