题目内容
5.已知M={x|x2-5x+6=0},N={x|ax=12},若N⊆M,求实数a所构成的集合A,并写出A的所有非空真子集.分析 化简M={x|x2-5x+6=0}={2,3},从而分类讨论求a的取值,再写出非空真子集.
解答 解:M={x|x2-5x+6=0}={2,3},
若N={x|ax=12}=∅,则N⊆M,此时a=0;
若N={x|ax=12}={2},则N⊆M,此时a=6;
若N={x|ax=12}={3},则N⊆M,此时a=4;
故A={0,4,6};
故A的所有非空真子集是{0},{4},{6},{0,4},{0,6},{4,6}.
点评 本题考查了集合的化简与应用,同时考查了分类讨论的思想应用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
16.若10-2x=25,则10x的值为( )
| A. | $±\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $-\frac{1}{5}$ | D. | $\frac{1}{625}$ |
20.函数$y=\sqrt{{{log}_{\frac{3}{4}}}(3x-1)}$的定义域是( )
| A. | [1,3] | B. | $({-∞,\frac{1}{3}}]$ | C. | $({\frac{1}{3},\frac{2}{3}}]$ | D. | $({\frac{2}{3},+∞})$ |
17.下列四个命题,其中是假命题的是( )
| A. | 不存在无穷多个角α和β,使得sin(α+β)=sinαcosβ-cosαsinβ | |
| B. | 存在这样的角α和β,使得cos(α+β)=cosαcosβ+sinαsinβ | |
| C. | 对任意角α和β,都有cos(α+β)=cosαcosβ-sinαsinβ | |
| D. | 不存在这样的角α和β,使得sin(α+β)≠sinαcosβ+cosαsinβ |
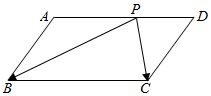 如图,在面积为4的平行四边形ABCD中,点P为直线AD上的动点,则$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值为4$\sqrt{3}$.
如图,在面积为4的平行四边形ABCD中,点P为直线AD上的动点,则$\overrightarrow{PB}•\overrightarrow{PC}+{\overrightarrow{BC}^2}$的最小值为4$\sqrt{3}$.