题目内容
设函数y=|2x-1|的定义域与值域均为[a，b]（b＞a），则a+b=
- A.1
- B.2
- C.3
- D.4
A
分析：先通过函数的值域看出a、b之间的关系，再根据函数f（x）在[0，+∞）上是单调递增，代入点的坐标建立方程组，
解答：∵f（x）=|2x-1|的值域为[a，b]，
∴b＞a≥0，
∵函数f（x）=|2x-1|在[0，+∞）上是单调递增函数，
∴把所给的两个点的坐标代入得到
，解得 
或
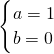（舍去）
∴有a+b=1．
故选A．
点评：本题考查了指数函数的定义域和值域，含绝对值函数的单调性，本题解题的关键是看出函数的单调性，从而可以建立方程组，本题是一个中档题目．
分析：先通过函数的值域看出a、b之间的关系，再根据函数f（x）在[0，+∞）上是单调递增，代入点的坐标建立方程组，
解答：∵f（x）=|2x-1|的值域为[a，b]，
∴b＞a≥0，
∵函数f（x）=|2x-1|在[0，+∞）上是单调递增函数，
∴把所给的两个点的坐标代入得到
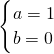，解得 或（舍去）∴有a+b=1．
故选A．
点评：本题考查了指数函数的定义域和值域，含绝对值函数的单调性，本题解题的关键是看出函数的单调性，从而可以建立方程组，本题是一个中档题目．
练习册系列答案
名校课堂系列答案
相关题目