设x1.x2.x3为是不同的自然数.求s=$\frac{{x} {1}}{1}$+$\frac{{x} {2}}{4}$+$\frac{{x} {3}}{9}$的最小值．题目和参考答案——青夏教育精英家教网—

题目内容

20．设x₁，x₂，x₃为是不同的自然数，求s=$\frac{{x}_{1}}{1}$+$\frac{{x}_{2}}{4}$+$\frac{{x}_{3}}{9}$的最小值．

分析根据代数式的特点分别对x₁，x₂，x₃取值，求出s的最小值即可．

解答解：x₁，x₂，x₃为是不同的自然数，
显然x₁=0，x₂=1，x₃=2时，
s=$\frac{{x}_{1}}{1}$+$\frac{{x}_{2}}{4}$+$\frac{{x}_{3}}{9}$的值最小，最小值是：
s=$\frac{0}{1}$+$\frac{1}{4}$+$\frac{2}{9}$=$\frac{17}{36}$．

点评本题考查了自然数的定义，考查求代数式的最小值问题，特殊值法是常用方法之一．

练习册系列答案

11．一个四面体的所有棱长都等于a，则该四面体的外接球的体积等于$\frac{\sqrt{6}}{8}$πa³．

8．已知函数f（x）=e^x-x²+2ax．
（1）若a=1，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若f（x）在R上单调递增，求实数a的取值范围．

15．设P是平行四边形ABCD的对角线的交点，O为任一点，则$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$+$\overrightarrow{OD}$=（　　）

A．

$4\overrightarrow{OP}$

B．

$3\overrightarrow{OP}$

C．

$2\overrightarrow{OP}$

D．

$\overrightarrow{OP}$

5．已知向量$\overrightarrow{a}$=（k，3），$\overrightarrow{b}$=（1，4），$\overrightarrow{c}$=（2，1）且（3$\overrightarrow{a}$-2$\overrightarrow{b}$）⊥$\overrightarrow{c}$，则实数k=（　　）

12．已知一个三棱锥的体积和表面积分别为V，S，若V=2，S=3，则该三棱锥内切球的表面积是16π．

9．已知p：方程$\frac{{x}^{2}}{9-m}$+$\frac{{y}^{2}}{2m}$=1表示焦点在x轴上的椭圆，q：双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{m}$=1的离心率e∈（$\frac{\sqrt{6}}{2}$，$\sqrt{2}$）．
（1）若椭圆$\frac{{x}^{2}}{9-m}$+$\frac{{y}^{2}}{2m}$=1的焦点和双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{m}$=1的顶点重合，求实数m的值；
（2）若“p∧q”是真命题，求实数m的取值范围．

10．

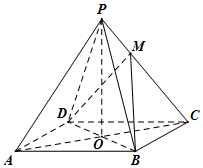如图，已知四棱锥P-ABCD的底面是菱形，对角线AC，BD交于点O，OA=4，OB=3，OP=4，OP⊥底面ABCD，设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$（λ＞0）．
（1）求当λ为何值时，使得PA∥平面BDM；
（2）当λ=$\frac{1}{2}$时，求直线PA与平面BDM所成角的正弦值；
（3）若二面角M-AB-C的大小为$\frac{π}{4}$，求λ的值．

试题分类