题目内容
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为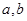 .
.
(Ⅰ)求直线 与圆
与圆 有公共点的概率;
有公共点的概率;
(Ⅱ)求方程组 只有正数解的概率。
只有正数解的概率。
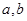 .
.(Ⅰ)求直线
 与圆
与圆 有公共点的概率;
有公共点的概率;(Ⅱ)求方程组
 只有正数解的概率。
只有正数解的概率。(Ⅰ)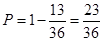 (Ⅱ)P(方程组只有正数解)=
(Ⅱ)P(方程组只有正数解)=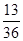
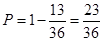 (Ⅱ)P(方程组只有正数解)=
(Ⅱ)P(方程组只有正数解)=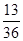
(Ⅰ)直线 与圆
与圆 有公共点的概率则圆心到直线的距离 小于半径,即
有公共点的概率则圆心到直线的距离 小于半径,即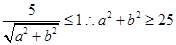 ,列出a,b的符合条件的情况,古典概型求解;
,列出a,b的符合条件的情况,古典概型求解;
方程组 ,的解为正,则
,的解为正,则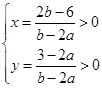 ,求出a,b的范围,列出即可。
,求出a,b的范围,列出即可。
解:(Ⅰ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为6×6=36.
因为直线ax+by+5=0与圆x2+y2=1有公共点,所以有
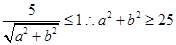 ,由于a,b∈{1,2,3,4,5,6}.
,由于a,b∈{1,2,3,4,5,6}.
∵满足条件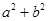 <25的情况(a,b)有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13种情况.
<25的情况(a,b)有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13种情况.
所以,直线ax+by+c=0与圆x2+y2=1有公共点的概率是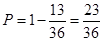 ---6分
---6分
(Ⅱ)由方程组 ,得
,得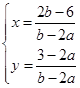
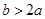 时,
时,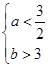 ,即
,即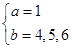 符合条件的数组
符合条件的数组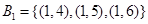 共有3个
共有3个
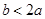 时,
时,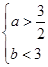 ,即
,即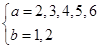 符合条件的数组
符合条件的数组
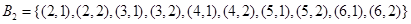 共有10个
共有10个
故P(方程组只有正数解)=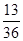
 与圆
与圆 有公共点的概率则圆心到直线的距离 小于半径,即
有公共点的概率则圆心到直线的距离 小于半径,即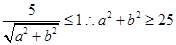 ,列出a,b的符合条件的情况,古典概型求解;
,列出a,b的符合条件的情况,古典概型求解;方程组
 ,的解为正,则
,的解为正,则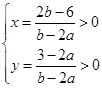 ,求出a,b的范围,列出即可。
,求出a,b的范围,列出即可。解:(Ⅰ)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为6×6=36.
因为直线ax+by+5=0与圆x2+y2=1有公共点,所以有
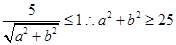 ,由于a,b∈{1,2,3,4,5,6}.
,由于a,b∈{1,2,3,4,5,6}.∵满足条件
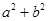 <25的情况(a,b)有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13种情况.
<25的情况(a,b)有(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13种情况.所以,直线ax+by+c=0与圆x2+y2=1有公共点的概率是
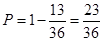 ---6分
---6分(Ⅱ)由方程组
 ,得
,得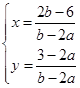
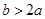 时,
时,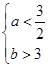 ,即
,即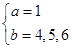 符合条件的数组
符合条件的数组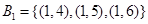 共有3个
共有3个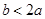 时,
时,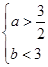 ,即
,即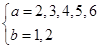 符合条件的数组
符合条件的数组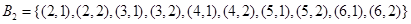 共有10个
共有10个故P(方程组只有正数解)=
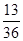

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
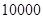 次还能继续使用的概率是
次还能继续使用的概率是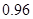 ,开关了
,开关了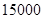 次后还能继续使用的概率是
次后还能继续使用的概率是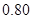 ,则已经开关了
,则已经开关了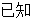 在
在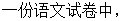 有四位不同的作者分别写了四篇不同的文章,题目要求答题者
有四位不同的作者分别写了四篇不同的文章,题目要求答题者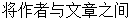 连线,每连对一组得2分,一名学生随意的一对一连线,设该生
连线,每连对一组得2分,一名学生随意的一对一连线,设该生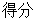 为
为 (1)求x=4及x=8时的概率;(2)求x≤2时的概率.
(1)求x=4及x=8时的概率;(2)求x≤2时的概率.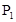 ,乙通过测试的概率为
,乙通过测试的概率为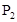 ,则甲、乙至少1人通过测试的概率为( )
,则甲、乙至少1人通过测试的概率为( )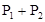
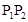
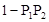
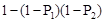
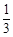 和
和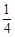 ,求(1)恰有1人译出密码的概率;
,求(1)恰有1人译出密码的概率; ,至少需要多少个乙这样的人?
,至少需要多少个乙这样的人?