题目内容
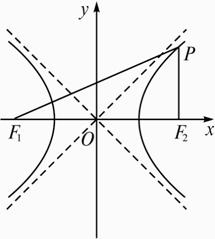
证明等轴双曲线x2-y2=a2上任意一点P到两焦点的距离的积等于P到中心距离的平方.
证明:焦点坐标分别为F1(-![]() a,0)、F2(
a,0)、F2(![]() a,0).
a,0).
设P点的坐标为(x,y),则x2-y2=a2.
故|PF1|=![]()
=![]()
=|![]() x+a|,
x+a|,
|PF2|=![]()
=![]()
=|![]() x-a|.
x-a|.
∴|PF1|·|PF2|=|![]() x+a|·|
x+a|·|![]() x-a|
x-a|
=|2x2-a2|=2x2-a2.
而|PO|2=x2+y2=2x2-a2,
∴|PF1|·|PF2|=|PO|2.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目