题目内容
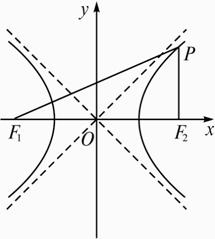
证明：等轴双曲线x2-y2=a2上任意一点P到它的两个焦点的距离的积等于点P到双曲线中心距离的平方.
思路解析：本题证法较多.法一，利用双曲线的焦半径公式证明.法二，直接用两点间的距离公式求出距离后证明.由x2-y2=a2得双曲线的离心率e= 证法一：|PF1|·|PF2|= |PF1|·|PF2|=| 证法二：|PF1|·|PF2|=|ex0+a|·|ex0-a|=|2x02-a2|=x02+y02=|OP|2. 证法三：|PF1|·|PF2|= = 方法归纳 等轴双曲线方程有两种情形，解题时注意分析焦点的位置.关于等轴双曲线的问题，解题思路同双曲线问题，解题时应充分利用“等轴”特征.
，焦点坐标为(±
a,0),设P（x0,y0）,则x02-y02=a2,∴x02-a2=y02.
·
,将x02-a2=y02代入得
x0+a|·|
x0-a|=|2x02-a2|=x02+y02=|OP|2.
=…=|OP|2.
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
相关题目
