题目内容

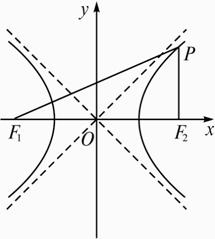
如图，设P为等轴双曲线x2-y2=1上的一点，F1、F2是两个焦点，

证明：|PF1|·|PF2|=|OP|2.

证明：设P（secφ,tanφ）,∵F1(-,0),F2(,0),?

∴|PF1|=

=

|PF2|=

=

|PF1|·|PF2|==2sec2φ-1.?

∵|OP|2=sec2φ+tan2φ=2sec2φ-1,

∴|PF1|·|PF2|=|OP|2.

练习册系列答案
相关题目
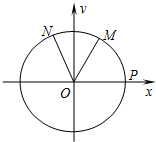精英家教网如图，设P是单位圆和x轴正半轴的交点，M、N是单位圆上的两点，O是坐标原点，∠POM=
π
3
，∠PON=α，α∈[0，π），f(α)=
OM
•
ON
，则f（a）的范围为（　　）
A、(-
1
2
，1]
B、[-
1
2
，
1
2
)
C、[-
1
2
，1)
D、(
1
2
，1)
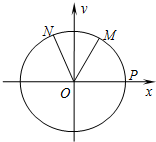精英家教网如图，设P是单位圆和x轴正半轴的交点，M、N是单位圆上的两点，O是坐标原点，∠POM=
π
3
，∠PON=α，α∈[0，π]，f(α)=|
OM
+
ON
|，则f（a）的范围为
 
．

如图所示，设P为等轴双曲线上的一点，、是两个焦点，证明：．
如图，设P为等轴双曲线x2-y2=1上的一点，F1、F2是两个焦点，

证明：|PF1|·|PF2|=|OP|2.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网