题目内容
已知A、B分别是x轴和y轴上的两个动点,满足|AB|=2,点P在线段AB上,且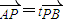 (t是不为0的常数),设点P的轨迹方程为C.
(t是不为0的常数),设点P的轨迹方程为C.(Ⅰ)求点P的轨迹方程C;
(Ⅱ)若曲线C为焦点在x轴上的椭圆,试求实数t的取值范围;
(Ⅲ)若t=2,点M、N是C上关于原点对称的两个动点,点Q的坐标为
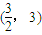 ,求△QMN的面积S的最大值.
,求△QMN的面积S的最大值.
【答案】分析:(Ⅰ)设点A(a,0),B(0,b),C(x,y),由题意知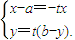 所以
所以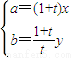 .再由|AB|=2,能够推出点P的轨迹方程.
.再由|AB|=2,能够推出点P的轨迹方程.
(Ⅱ)由题意知,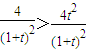 ,解可得答案;
,解可得答案;
(Ⅲ)当t=2时,曲线C的方程为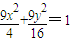 ,设M(x1,y1),N(-x1,-y1),则
,设M(x1,y1),N(-x1,-y1),则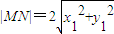 .设直线MN的方程为
.设直线MN的方程为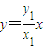 ,所以点Q到直线MN的距离
,所以点Q到直线MN的距离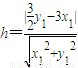 ,由此可求出△QMN的面积S的最大值.
,由此可求出△QMN的面积S的最大值.
解答:解:(Ⅰ)设点A(a,0),B(0,b),C(x,y),
∵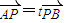 ,即(x-a,y)=t(-x,b-y),即
,即(x-a,y)=t(-x,b-y),即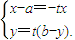 (2分)
(2分)
则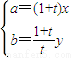 .
.
又∵|AB|=2,即a2+b2=4.
∴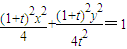 .
.
∴点P的轨迹方程C: .(5分)
.(5分)
(Ⅱ)∵曲线C为焦点在x轴上的椭圆,
∴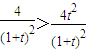 ,得t2<1.
,得t2<1.
又∵t>0,∴0<t<1.(8分)
(Ⅲ)当t=2时,曲线C的方程为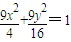 .(9分)
.(9分)
设M(x1,y1),N(-x1,-y1),则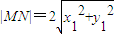 .
.
当x1≠0时,设直线MN的方程为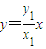 ,
,
则点Q到直线MN的距离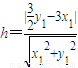 ,
,
∴△QMN的面积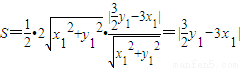 .(11分)
.(11分)
∴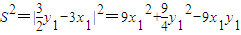 .
.
又∵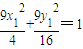 ,
,
∴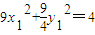 .
.
∴S2=4-9x1y1.
而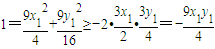 ,
,
则-9x1y1≤4.即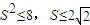 .
.
当且仅当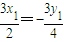 时,
时,
即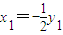 时,“=”成立.
时,“=”成立.
当x1=0时,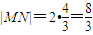 ,
,
∴△QMN的面积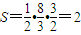 .
.
∴S有最大值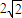 .(14分)
.(14分)
点评:本题考查直线的圆锥曲线的综合应用,解题时要认真审题,仔细解答.
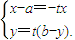 所以
所以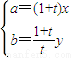 .再由|AB|=2,能够推出点P的轨迹方程.
.再由|AB|=2,能够推出点P的轨迹方程.(Ⅱ)由题意知,
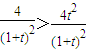 ,解可得答案;
,解可得答案;(Ⅲ)当t=2时,曲线C的方程为
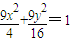 ,设M(x1,y1),N(-x1,-y1),则
,设M(x1,y1),N(-x1,-y1),则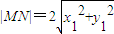 .设直线MN的方程为
.设直线MN的方程为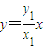 ,所以点Q到直线MN的距离
,所以点Q到直线MN的距离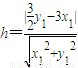 ,由此可求出△QMN的面积S的最大值.
,由此可求出△QMN的面积S的最大值.解答:解:(Ⅰ)设点A(a,0),B(0,b),C(x,y),
∵
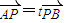 ,即(x-a,y)=t(-x,b-y),即
,即(x-a,y)=t(-x,b-y),即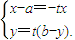 (2分)
(2分)则
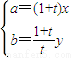 .
.又∵|AB|=2,即a2+b2=4.
∴
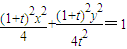 .
.∴点P的轨迹方程C:
 .(5分)
.(5分)(Ⅱ)∵曲线C为焦点在x轴上的椭圆,
∴
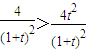 ,得t2<1.
,得t2<1.又∵t>0,∴0<t<1.(8分)
(Ⅲ)当t=2时,曲线C的方程为
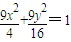 .(9分)
.(9分)设M(x1,y1),N(-x1,-y1),则
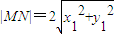 .
.当x1≠0时,设直线MN的方程为
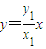 ,
,则点Q到直线MN的距离
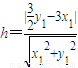 ,
,∴△QMN的面积
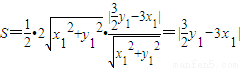 .(11分)
.(11分)∴
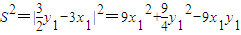 .
.又∵
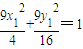 ,
,∴
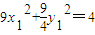 .
.∴S2=4-9x1y1.
而
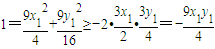 ,
,则-9x1y1≤4.即
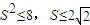 .
.当且仅当
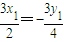 时,
时,即
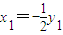 时,“=”成立.
时,“=”成立.当x1=0时,
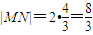 ,
,∴△QMN的面积
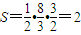 .
.∴S有最大值
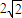 .(14分)
.(14分)点评:本题考查直线的圆锥曲线的综合应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 ,设点P的轨迹方程为C.
,设点P的轨迹方程为C.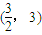 ,求△QMN的面积S的最大值.
,求△QMN的面积S的最大值.